Problema di relatività ristretta.
Scusate ragazzi se questa non é la sezione giusta in cui postare un problema di relatività ristretta, ma spero ci sia qualcuno che possa aiutare.
Questo il testo del problema:
Un sistema di riferimento inerziale S’ si muove con velocità v = 0,640 c, nel verso delle
ascisse (positive) di entrambi i sistemi, rispetto a un secondo sistema di riferimento
inerziale S, in configurazione standard con S’. Quando gli orologi dei due sistemi segnano
il valore t = t’ = 0 s un osservatore A si trova fermo in S nel punto xA = d = 2,12 * 109m.
All'istante t1 = 6,02 s di S, l’osservatore A fa partire un lampo di luce.
a) Qual è, secondo A, il tempo t’1 segnato dagli orologi di S’ nel momento in cui parte
il lampo?
b) Qual è la posizione iniziale di A secondo le misure effettuate in S’ ?
c) Qual è la posizione di x’A di A, in S’, all'istante t’1 ?
d) Considera l'evento di S’ ≪ l'osservatore A si trova in x’=x ‘A all'istante t = t ‘1 ≫ .
Quali sono le coordinate dello stesso evento nel sistema di riferimento S?
Ringrazio tutti quelli che vorranno dedicare un po' del loro tempo a risolvere il quesito😁
Re: Problema di relatività ristretta.
la sincronizzazione degli orologi di due osservatori può essere fatta solo quando gli osservatori sono fermi oppure se occupano la stessa posizione in modo che ognuno abbia accesso all'orologio dell'altro
mi sembra invece che nel tuo esempio all'istante t = t' = 0 i due osservatori sono distanti e in movimento
i loro orologi non possono essere sincronizzati
Re: Problema di relatività ristretta.
Vero, ma il problema non dice che vengono sincronizzati. Dice solo il tempo indicato dai due orologi e dà la coordinata spaziale di un osservatore rispetto ad S,dicendo che è fermo rispetto ad esso.
Re: Problema di relatività ristretta.
Citazione:
Originariamente Scritto da
Andre21

Scusate ragazzi se questa non é la sezione giusta in cui postare un problema di relatività ristretta, ma spero ci sia qualcuno che possa aiutare.
Questo il testo del problema:
Un sistema di riferimento inerziale S’ si muove con velocità v = 0,640 c, nel verso delle
ascisse (positive) di entrambi i sistemi, rispetto a un secondo sistema di riferimento
inerziale S, in configurazione standard con S’. Quando gli orologi dei due sistemi segnano
il valore t = t’ = 0 s un osservatore A si trova fermo in S nel punto xA = d = 2,12 * 109m.
All'istante t1 = 6,02 s di S, l’osservatore A fa partire un lampo di luce.
a) Qual è, secondo A, il tempo t’1 segnato dagli orologi di S’ nel momento in cui parte
il lampo?
La formula per la dilatazione dei tempi è 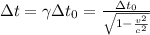 .
.
Tenendo conto che per A è il sistema S' a muoversi a V= 0.64 c, il suo tempo sarà rallentato e, usando i dati riferiti e la formula, sarà pari a 4.63 secondi.
Citazione:
b) Qual è la posizione iniziale di A secondo le misure effettuate in S’ ?
La formula per la contrazione delle lunghezze è 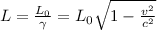 .
.
Per S' è A che è in movimento, quindi la distanza si contrae e, dai dati riferiti e la formula, sarà pari a 1.63 * 109 m.
Citazione:
c) Qual è la posizione di x’A di A, in S’, all'istante t’1 ?
In S', t'1 è l'istante in cui A fa partire il lampo di luce. Poiché per S' è il tempo di A a rallentare, il lampo non è partito dopo 6.02 s ma, per la dilatazione dei tempi, è partito a 7.83 s.
Dopo 7.83 s a V=0.64 c, A si sarà mosso di 1.5 * 109 m che, sommati ai precedenti 1.63 * 109 m, fanno 3.13 *109 m.
Citazione:
d) Considera l'evento di S’ ≪ l'osservatore A si trova in x’=x ‘A all'istante t = t ‘1 ≫ .
Quali sono le coordinate dello stesso evento nel sistema di riferimento S?
L'istante t'1 è l'attimo in cui A fa partire il lampo di luce. Per S' A si muove, ma per S no. Dunque, per S, A è sempre alla stessa distanza e sono passati 6.02 s.
Citazione:
Ringrazio tutti quelli che vorranno dedicare un po' del loro tempo a risolvere il quesito��
Di nulla.;)
Re: Problema di relatività ristretta.
I calcoli naturalmente sono corretti ma ho qualche dubbio sulla consistenza del problema stesso
gli orologi di due osservatori in moto relativo non sono sincronizzati
Supponiamo che S ed S' si incrocino
Solo in questo istante i due osservatori possono avere accesso all'orologio dell'altro
supponiamo che S imposti il proprio orologio a t0 = -10 e S' a t'0 = -7.69
Trascorsi 10 sec secondo S si avrà t = 0 e t' = 0, i due osservatori si sono allontanati
Dovremmo aver riprodotto la condizione iniziale del problema, per la distanza basta naturalmente aggiustare t0 e t'0
i due osservatori però non sarebbero più simmetrici
Re: Problema di relatività ristretta.
Intanto ringrazio tutti per l'interesse che state mostrando.
Io credo che il problema stesso sia scorretto e chiedo il vostro parere su questo ragionamento. Le trasformazioni di Lorentz, da cui si ricavano le note relazioni di contrazione delle lunghezze e dilatazione degli intervalli temporali, sono trasformazioni lineari ed omogenee nelle variabili spaziotemporali. Scritte per sistemi in configurazione standard infatti danno che al tempo t=0 ed x=0 misurati in S, anche x' e t' misurati in S' debbano essere nulli. Ora il testo mi dice che i sistemi erano in configurazione standard però mi dice anche che quando per S l'osservatore A si trova in x=2.22x10^9 al tempo t=0, per S' il tempo misurato è t'=0. Ma in questo caso è facile vedere che le trasformazioni di Lorentz non possono venire soddisfatte dalle coordinate date. Se nella trasformazione della x, pongo t=0 ricavo x'=\gamma x. Dalla trasformazione della variabile temporale ponendo t=0 essendo la x di A non nulla, ricaverei un tempo t' negativo, non nullo come indicato problema.Quindi direi che i sistemi S ed S' non possono essere in configurazione standard. Che le trasformazioni tra le loro coordinate non sono più quelle di Lorentz ma quelle di Poincare di cui quelle di Lorentz sono un caso particolare.
Fermo restando che le relazioni della dilatazione temporale e contrazione delle lunghezze rimangono valide anche sotto trasformazioni di Poincare. Ritengo il problema ambiguo. Vorrei verificare che sia per l'evento "POSIZIONE SPAZIOTEMPORALE DI A" che per l'evento " EMISSIONE DEL LAMPO DI LUCE " la norma del quadrivettore spaziotempo rimanga invariata misurata dai due sistemi.Ma se prendo per l'evento emissione del lampo, in S le coordinate (2.12x10^9;6.02) e le trasformate calcolate come da Albertus (3.13x10^9;7.83) la norma del quadrivettore non si conserva. Correggetemi se ho sbagliato qualcosa, grazie.
Re: Problema di relatività ristretta.
non sono cosi versato nella teoria della relatività da dare una risposta definitiva
Io sapevo che le equazioni di Lorentz valgono a condizione che i due sistemi in moto relativo condividano la stessa origine agli istanti t = t' = 0
Quindi mi era squillato un campanello d'allarme
comunque il gruppo di Lorentz : ds^2 = c*dt^2 -dx^2 - dy^2 - dz^2 gode della proprietà di esser covariante per tutte le trasformazioni spazio temporali
La grande intuizione di Einstein fu proprio questa:
Le leggi della natura devono esser indipendenti dal sistema di riferimento
Due osservatori, in moto relativo, possono avere valoro diversi di dt, dx,dy,dz ma hanno lo stesso ds
Detto prosaicamente i due osservatori dovranno pure avere qualcosa in comune altrimenti cadremmo nel relativismo assoluto vale a dire in una concezione metafisica della natura
Il gruppo di Lorentz è un sotto gruppo del gruppo di Poincarè, questo però non implica necessariamente che una struttura matematica debba avere un corrispettivo nel mondo naturale
I fisici scelgono le strutture matematiche che ritengono coerenti con la loro visione o intuizione del mondo fisico per poi sottoporle al giudizio inappellabile dell'esperienza
Forse il gruppo di Poincare non risponde a questi requisiti
Per questo, come ho avuto modo di dire in un'altra discussione, , a mio giudizio, se si vuole afferrare la teoria della relatività speciale non si può prescindere dal gruppo di Lorentz e del relativo " intervallo spazio temporale" ds
La pedissequa applicazione delle equazioni di Lorentz può essere fuorviante
Non mi ero mai posto il problema del "super gruppo " di Poincare, adesso mi hai messo la pulce nell'orecchio :)
Re: Problema di relatività ristretta.
Citazione:
Originariamente Scritto da
Albertus

I calcoli naturalmente sono corretti ma ho qualche dubbio sulla consistenza del problema stesso
gli orologi di due osservatori in moto relativo non sono sincronizzati
Supponiamo che S ed S' si incrocino
Solo in questo istante i due osservatori possono avere accesso all'orologio dell'altro
supponiamo che S imposti il proprio orologio a t0 = -10 e S' a t'0 = -7.69
Trascorsi 10 sec secondo S si avrà t = 0 e t' = 0, i due osservatori si sono allontanati
Dovremmo aver riprodotto la condizione iniziale del problema, per la distanza basta naturalmente aggiustare t0 e t'0
i due osservatori però non sarebbero più simmetrici
Il problema posto non suppone una sincronizzazione, ma una constatazione di fatto.
Quando i due sistemi si incrociano osserviamo i due orologi: anche se S segna 3 min e S' segna 3 s, a noi basta stabilire per convenzione che t0 per S è pari a 3 min, e t'0 per S' è pari a 3 s.
Quando andiamo ad effettuare i calcoli della RS sui tempi, calcoliamo i 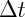 (le differenze di tempi), non i tempi assoluti (che non esistono).
(le differenze di tempi), non i tempi assoluti (che non esistono).
Quindi, anche se i due orologi segnano tempi diversi, possiamo convenzionalmente stabilire che segnino 0 al loro incontro, perchè comunque la cosa è ininfluente ai fini dei calcoli.
L'importante è ricordarsi che parliamo di una convenzione, non di una sincronizzazione...;)
Re: Problema di relatività ristretta.
Citazione:
Originariamente Scritto da
Andre21

Intanto ringrazio tutti per l'interesse che state mostrando.
Io credo che il problema stesso sia scorretto e chiedo il vostro parere su questo ragionamento. Le trasformazioni di Lorentz, da cui si ricavano le note relazioni di contrazione delle lunghezze e dilatazione degli intervalli temporali, sono trasformazioni lineari ed omogenee nelle variabili spaziotemporali. Scritte per sistemi in configurazione standard infatti danno che al tempo t=0 ed x=0 misurati in S, anche x' e t' misurati in S' debbano essere nulli. Ora il testo mi dice che i sistemi erano in configurazione standard però mi dice anche che quando per S l'osservatore A si trova in x=2.22x10^9 al tempo t=0, per S' il tempo misurato è t'=0. Ma in questo caso è facile vedere che le trasformazioni di Lorentz non possono venire soddisfatte dalle coordinate date. Se nella trasformazione della x, pongo t=0 ricavo x'=\gamma x. Dalla trasformazione della variabile temporale ponendo t=0 essendo la x di A non nulla, ricaverei un tempo t' negativo, non nullo come indicato problema.Quindi direi che i sistemi S ed S' non possono essere in configurazione standard. Che le trasformazioni tra le loro coordinate non sono più quelle di Lorentz ma quelle di Poincare di cui quelle di Lorentz sono un caso particolare.
Fermo restando che le relazioni della dilatazione temporale e contrazione delle lunghezze rimangono valide anche sotto trasformazioni di Poincare. Ritengo il problema ambiguo. Vorrei verificare che sia per l'evento "POSIZIONE SPAZIOTEMPORALE DI A" che per l'evento " EMISSIONE DEL LAMPO DI LUCE " la norma del quadrivettore spaziotempo rimanga invariata misurata dai due sistemi.Ma se prendo per l'evento emissione del lampo, in S le coordinate (2.12x10^9;6.02) e le trasformate calcolate come da Albertus (3.13x10^9;7.83) la norma del quadrivettore non si conserva. Correggetemi se ho sbagliato qualcosa, grazie.
Come ho detto prima, i calcoli si fanno sui 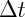 , non sui tempi assoluti. E' importante ricordare che parliamo di DIFFERENZE in termine di misura dei tempi.
, non sui tempi assoluti. E' importante ricordare che parliamo di DIFFERENZE in termine di misura dei tempi.
E' quindi ovvio che, stabilendo un 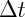 pari a zero, le trasformate non funzionino.
pari a zero, le trasformate non funzionino.
Ti faccio inoltre notare che 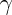 si calcola anche facendo il rapporto tra i quadrati della velocità v relativa e la velocità della luce c. Ma la velocità è un rapporto tra lo spazio percorso in un determinato tempo, e se poni un tempo pari a 0, anche concettualmente non puoi stabilire una velocità.;)
si calcola anche facendo il rapporto tra i quadrati della velocità v relativa e la velocità della luce c. Ma la velocità è un rapporto tra lo spazio percorso in un determinato tempo, e se poni un tempo pari a 0, anche concettualmente non puoi stabilire una velocità.;)
Re: Problema di relatività ristretta.
la definizione di configurazione standard è chiara
le origini degli assi devono coincidere se t = t' = 0
Le equazioni di Lorentz valgono solo in configurazione standard
a meno che non si intenda che esiste un osservatore A fermo in xA = d = 2,12 * 109m. rispetto al sistema S
ma l'origine di S e S' coincidono all'istante t = t' =0
L'origine dei tempi e l'origine delle misure spaziali devono essere gli stessi
i


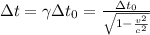 .
.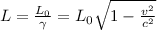 .
.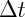 (le differenze di tempi), non i tempi assoluti (che non esistono).
(le differenze di tempi), non i tempi assoluti (che non esistono).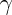 si calcola anche facendo il rapporto tra i quadrati della velocità v relativa e la velocità della luce c. Ma la velocità è un rapporto tra lo spazio percorso in un determinato tempo, e se poni un tempo pari a 0, anche concettualmente non puoi stabilire una velocità.;)
si calcola anche facendo il rapporto tra i quadrati della velocità v relativa e la velocità della luce c. Ma la velocità è un rapporto tra lo spazio percorso in un determinato tempo, e se poni un tempo pari a 0, anche concettualmente non puoi stabilire una velocità.;)