-
Il modello cosmologico standard ?CDM - Parte III: storia e proprietà della CBR
Continuando il nostro viaggio nella struttura e formazione dell'Universo, affronteremo in questa nuova parte uno delle evidenze osservative più importanti della cosmologia, la radiazione cosmica di fondo, ovvero l'eco del Big Bang. Ne descriveremo dunque le proprietà, l'origine e le osservazioni che ci hanno permesso di studiarla in modo così approfondito. Questo ci servirà per avere le b...
leggi tutto...
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Per @Cyg X-1, questa è la terza parte che dovrebbe essere di tuo interesse. Ne seguiranno ancora altre, probabilmente altre 3 o 4.
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Interessante il discorso della polarizzazione della cmb...
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Citazione:
Originariamente Scritto da
DarknessLight

Interessante il discorso della polarizzazione della cmb...
Hai visto Dark? Stavolta niente formule...anzi solo una ma molto semplice :angel:.
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
La CBR ha una piccola parte polarizzata, ovvero una porzione della radiazione cosmica ha un campo elettrico che oscilla in direzioni ben precise. Questo studio è attualmente in fase di sviluppo e permetterà ai cosmologi di aggiungere ulteriore dettaglio per vincolare il modello cosmologico che descrive l’Universo.
@Enrico Corsaro
Hai qualche info in più al riguardo? Questa polarizzazione rappresenta forse un anisotropia di qualche tipo?
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
La polarizzazione della CBR è da un punto di vista teorico legata a due tipi di effetti. Il primo prende il nome di modi E, e sono legati al processo di diffusione Thomson nel plasma (già osservati nel 2002), gli altri sono i modi B, che possono essere causati da due tipi di fenomeni fisici, il primo è per effetto del lensing gravitazionale dei modi E (anch'esso già osservato nel 2013), ed il secondo è per effetto delle onde di gravità dovute all'inflazione, il così discusso dibattito di BICEP2, come probabilmente ne avrai sentito parlare. E' stato infatti proporio grazie a Planck che la possibile rivelazione dei modi B dati dall'inflazione grazie alle osservazioni dal polo di BICEP2, è stata stroncata.
Le analisi continuano in questa direzione, si vedrà dunque in futuro se ci saranno nuovi studi.
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
@Enrico Corsaro, come hai detto la radiazione di fondo è quasi uguale a quella caratteristica di un corpo nero. Questo "quasi" mi stuzzica: ci si può ricavare qualche informazione?:thinking:
-
Allegati: 1
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Citazione:
Originariamente Scritto da
Red Hanuman

@
Enrico Corsaro, come hai detto la radiazione di fondo è quasi uguale a quella caratteristica di un corpo nero. Questo "quasi" mi stuzzica: ci si può ricavare qualche informazione?:thinking:
Caro Red, essenzialmente il quasi l'ho utilizzato perchè in natura nulla è perfettamente uguale a come noi lo modellizziamo. Tuttavia per la CBR la parola "perfetto" è molto più appropriata che in altri contesti. Come ti mostra questa figura dello spettro di radiazione di corpo nero, la curva modellizzata passa perfettamente entro tutti i punti osservati. Con passa perfettamente intendo sempre entro le barre di errore. Per cui la risposta alla tua domanda è che in questo caso non è possibile ricavare alcuna informazione sensibile da eventuali piccole dieviazioni, dal momento che le barre di errore sui punti osservati sono della stessa grandezza, se non addirittura ben più grandi, delle deviazioni del modello :).Allegato 12488
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Ciao Enrico.
Nell’articolo si parla delle anisotropie presentate dalla RCF, esclusivamente in relazione a differenze di temperatura ma non in relazione a differenze di intensità.
Da perfetto profano mi aspetto che almeno le fluttuazioni secondarie (quelle cioè provocate dalla maggiore densità di materia incontrata dalla RCF nel suo vagabondaggio cosmico) prevedano un assorbimento, più o meno importante, della RCF che quindi dovrebbe apparire meno densa (minor numero di fotoni per metro cubo di spazio) in direzione dei superammassi di galassie. Ciò effettivamente avviene sul piano galattico per effetto degli assorbimenti prodotti dalla Via Lattea, ma, per il resto del cosmo, accade la stessa cosa? E’ possibile, in linea di principio, stabilire la distribuzione delle galassie ricorrendo a questo tipo di analisi?
Un’altra questione cosmologica in qualche modo connessa alla RCF, è la seguente:
Ti chiedo se esiste una relazione matematica che indichi il raffreddamento dell’universo (ovvero la variazione della temperatura della RCF) in funzione del tempo. Siamo partiti da circa 3.000K (praticamente la temperatura superficiale di una nana rossa) con T=380.000 anni per arrivare agli attuali 2,27K con T=14,3 mld di anni: in mezzo cosa c’è e come è variato?
Ed inoltre,
combinando la legge di variazione del fattore di scala (aumento nel tempo delle dimensioni dell’universo) che, nel caso più accreditato di modello piatto, cioè in lenta espansione, vale a(T)=(T/T0)^2/3,
con quella della temperatura, non si potrebbe ottenere la legge del raffreddamento dell’universo in funzione delle sue dimensioni?
Si lo so, sto trattando il cosmo come se fosse una sferetta di laboratorio di cui valutare il raffreddamento ponendole a contatto un termometro…. :shock: ma sono sicuro che i cosmologi qualche ideuzza ce l’hanno …. ;)
A me interessano le formule, caro Enrico, sempreché non siano troppo complicate. Mi piace divertirmi a disegnare grafici, anche se vanno presi con le molle; servono comunque a farsi un’idea di come vanno – almeno qualitativamente – le cose.
Grazie per l’attenzione e la … pazienza! :rolleyes:
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Ottimi spunti @Cyg X-1, vediamo di risponderti.
Citazione:
Originariamente Scritto da
Cyg X-1

Nell’articolo si parla delle anisotropie presentate dalla RCF, esclusivamente in relazione a differenze di temperatura ma non in relazione a differenze di intensità.
Da perfetto profano mi aspetto che almeno le fluttuazioni secondarie (quelle cioè provocate dalla maggiore densità di materia incontrata dalla RCF nel suo vagabondaggio cosmico) prevedano un assorbimento, più o meno importante, della RCF che quindi dovrebbe apparire meno densa (minor numero di fotoni per metro cubo di spazio) in direzione dei superammassi di galassie. Ciò effettivamente avviene sul piano galattico per effetto degli assorbimenti prodotti dalla Via Lattea, ma, per il resto del cosmo, accade la stessa cosa? E’ possibile, in linea di principio, stabilire la distribuzione delle galassie ricorrendo a questo tipo di analisi?
Il problema di base qui è che la quantità di fotoni media che riceviamo dalla CBR è davvero molto bassa a confronto con tutte le altre sorgenti. Questo comporta in generale problemi nell'utilizzare l'informazione fotonica come numero fisico per fare deduzioni sulla distribuzione di materia che la CBR ha attraversato. Inoltre è praticamente impossibile separare la CBR da altre fonti di radiazioni semplicemente sulla base del numero di fotoni.
Mi spiego meglio.
Immagina di guardare in una sola direzione e di acquisire un segnale fotonico. In questo segnale ipotizziamo che sia contenuta sia la CBR che ad esempio l'emissione di una galassia localizzata proprio nel campo che stiamo inquadrando. Di base acquisendo semplicemente un conteggio del numero di fotoni non riusciamo a capire quanti provengano dalla CBR e quanti dalla galassia, è una informazione completamente amalgamata. Paradossalmente, se non sapessimo della CBR e dato il suo basso numero di fotoni per centimetrocubo, neanche potremmo mai dedurre che essa sia presente utilizzando un metodo simile. Capisci dunque che non abbiamo alcun modo di disaccoppiare le due sorgenti guardando solo al numero di fotoni. L'unico modo di distinguere sorgenti diverse è di analizzare invece le proprietà della radiazione in termini energetici e di polarizzazione. Infatti l'informazione di cui tu parli te la da proprio la fluttuazione in temperatura, che possiamo misurare con molta precisione e accuratezza, proprio perchè è principalmente l'energia dei fotoni a cambiare nei processi di assorbimento e riemissione che avvengono quando la CBR attraversa ad esempio un ammasso di galassia.
Citazione:
Originariamente Scritto da
Cyg X-1

Un’altra questione cosmologica in qualche modo connessa alla RCF, è la seguente:
Ti chiedo se esiste una relazione matematica che indichi il raffreddamento dell’universo (ovvero la variazione della temperatura della RCF) in funzione del tempo. Siamo partiti da circa 3.000K (praticamente la temperatura superficiale di una nana rossa) con T=380.000 anni per arrivare agli attuali 2,27K con T=14,3 mld di anni: in mezzo cosa c’è e come è variato?
Ed inoltre,
combinando la legge di variazione del fattore di scala (aumento nel tempo delle dimensioni dell’universo) che, nel caso più accreditato di modello piatto, cioè in lenta espansione, vale a(T)=(T/T0)^2/3,
con quella della temperatura, non si potrebbe ottenere la legge del raffreddamento dell’universo in funzione delle sue dimensioni?
A queste domande possiamo sostanzialmente fornire una risposta unica. La densità di energia della radiazione decresce con la quarta potenza del tempo, ovvero un fattore 1 più rapidamente di quanto non decresca una densità volumetrica, come quella della materia ad esempio. Avevamo discusso in parte questo discorso nella Parte I di questa serie, che trovi QUI. Ti fornisco a seguire qualche dettaglio in più usando delle semplici relazioni.
Considerando il fattore di scala a(t) come di fatto il "raggio" del nostro Universo in espansione, possiamo visualizzare le seguenti informazioni.
La densità di energia di materia in funzione del fattore di scala cosmico è
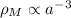
dove a3 è proporzionale al volume dell'Universo in base alle coordinate cosmologiche standard. Dunque una densità di energia di materia, cioè il numero di particelle per volume, che chiamo nM è proporzionale all'inverso del volume stesso, cioè
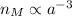
Sostituendo il risultato dall'integrazione dell'equazione di Friedmann che hai già citato, per cui
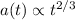
ottieni in definitiva che
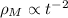
Per la radiazione invece dobbiamo considerare due effetti combinati.
1) la densità fotonica, analoga alla densità di particelle di materia per volume, è anch'essa data come
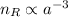
cioè proporzionale all'inverso del volume, ma a questo effetto si aggiunge
2) lo stiramento della lunghezza d'onda dovuto all'espansione dell'Universo, che è espresso nel redshift cosmologico. Il redshift cosmologico in funzione del fattore di scala cosmico è espresso come
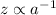
cioè il redshift aumenta con l'inverso del fattore scala.
Combinando i due effetti per la radiazione otteniamo in totale che
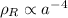
Questo è il motivo per cui la radiazione, dominante nei primissimi istanti di vita dell'Universo, è rapidamente passata in secondo piano, diventando energeticamente pari alla materia nell'epoca della ricombinazione.
Sostituendo a quest'ultima ancora una volta la dipendenza dal tempo dell'Equazione di Friedmann, otteniamo
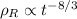
Citazione:
Originariamente Scritto da
Cyg X-1

Si lo so, sto trattando il cosmo come se fosse una sferetta di laboratorio di cui valutare il raffreddamento ponendole a contatto un termometro…. :shock: ma sono sicuro che i cosmologi qualche ideuzza ce l’hanno …. ;)
A me interessano le formule, caro Enrico, sempreché non siano troppo complicate. Mi piace divertirmi a disegnare grafici, anche se vanno presi con le molle; servono comunque a farsi un’idea di come vanno – almeno qualitativamente – le cose.
Grazie per l’attenzione e la … pazienza! :rolleyes:
Certamente fai bene, apprezzo che qualcuno abbia l'interesse di andare un pò più in dettaglio e tirare anche in ballo qualche equazione. Fammi sapere se le spiegazioni sono state chiare e grazie a te ;).
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Grazie Enrico, ad occhio e croce mi sembra di avere parecchi argomenti di riflessione.
Me li leggo con calma dopodichè mi rifarò sicuramente vivo. ;)
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
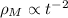
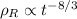
Ho provato a disegnare le due curve in funzione del tempo assegnando una costante di proporzionalità fittizia. Effettivamente la curva della densità di radiazione presenta una pendenza più elevata dell'altra per piccoli valori dell'ascissa (il tempo), mentre le cose s'invertono per alti valori del tempo cosmico (universo attuale).
Mi sembra che questo confermi la tua conclusione, ovvero della maggiore "importanza" della radiazione nell'universo giovane rispetto all'attuale.
Volevo però chiederti i valori delle due costanti di proporzionalità: cioè della densità di radiazione rispetto al tempo e della densità di materia rispetto al tempo, in modo da disegnare le curve in modo più realistico. Naturalmente spero che indicherai i passaggi necessari ad ottenerle .... abbi pazienza, io sono un pò come DarknessLight, quando comincio a rompere ...... :biggrin:). Scherzo DarknessLight, trovo anzi fondamentali le tue domande di approfondimento.
Grazie
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Quantificare la costante di proporzionalità è molto meno semplice del ricavare la proporzionalità stessa. Fisicamente è di fatto un problema di non poco conto, perchè calcolare la costante significa conoscere con precisione la quantità di materia e radiazione presente nell'Universo.
Per farlo occorre partire da tre informazioni fondamentali.
- Il bilancio energetico della materia nel budget totale al tempo odierno, secondo il modello cosmologico standard
- Il valore della densità di energia critica per un universo a geometria Euclidea
- La funzione esatta del fattore di scala cosmico in funzione del tempo per una costante cosmologica nulla, ed una geometria Euclidea, data da
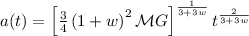
dove 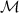 è la quantità totale di materia nell'Universo, G la costante di gravitazione universale, e il coefficiente dell'equazione di stato cosmologica
è la quantità totale di materia nell'Universo, G la costante di gravitazione universale, e il coefficiente dell'equazione di stato cosmologica 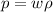 , pari a w = 0 per un Universo dominato da polveri, w = 1/3 se dominato da radiazione, w = 1 per Stiff matter, cioè materia rigida, come quella di un Universo primordiale estremamente denso.
, pari a w = 0 per un Universo dominato da polveri, w = 1/3 se dominato da radiazione, w = 1 per Stiff matter, cioè materia rigida, come quella di un Universo primordiale estremamente denso.
I primi due fattori li abbiamo già presentati nella Parte I. Prova intanto a vedere se riesci a venirne a capo e appena ho un pò più di tempo vediamo di ragionarci insieme se non riesci ;).
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Sono convinto che finirò per dire delle cavolate. Però non ne vengo a capo... La radiazione cosmica di fondo è stata emessa tra i 380.000 e i 400.000 anni do il B. B., ad una temperatura di 3000 °K. Quelle che noi consideriamo è quella che fa riferimento a queste condizioni e a quel particolare momento. Poi ha continuato ad mettere cambiando, naturalmente, le condizioni iniziali come tempo, temperatura, distanza e dimensione dell'universo primordiale. Ora noi la radiazione la vediamo arrivare da tutte le direzioni dell'universo osservabile come diretta conseguenza dell'espansione dell'universo a partire dal B.B. La domanda è fino a quando contoinueremo a vedere questo segnale? Come dovrebbe cambiare, se cambia, nel corso del tempo? Perchè lo stiamo vedendo adesso (a partire da quando Penzias e Wilson l'hanno rilevato) e non ne siamo stati scavalcati nel passato?
Disponibile a sentirmene dire di tutti i colori, ben venga qualsiasi contributo.:sad:
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Ragazzi, la cmb permea l intero cosmo perchè è un residuo OMOGENEO. più guardiamo lontano più la vediamo per come era all inizio quindi calda e densa, fino a che non riusciamo più a penetrare con le osservazioni visto che arriviamo a 380 000 anni dopo il Big bang, ovvero quando la radiazione era unita alla materia e quindi non poteva esistere interazione elettromagnetica che ci possa permettere di vedere!!
È GENIALE l analogia della coltre di nubi che viene riportata nell articolo di Enrico.
Invece se guardiamo vicino a noi vediamo la radiazione come è oggi ovvero fredda e rarefatta.
Insomma, so che non è proprio una perfetta analogia, ma la cmb alla fine è un po come le nubi di idrogeno ed elio cosmologici, che man mano che l universo si espande diventano fredde e rarefatte, ma se guardiamo lontano le vediamo dense e calde. Lo stesso vale per la radiazione!
Citazione:
Originariamente Scritto da
Cyg X-1

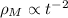
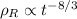
Ho provato a disegnare le due curve in funzione del tempo assegnando una costante di proporzionalità fittizia. Effettivamente la curva della densità di radiazione presenta una pendenza più elevata dell'altra per piccoli valori dell'ascissa (il tempo), mentre le cose s'invertono per alti valori del tempo cosmico (universo attuale).
Non serve che le disegni!
Basta una semplice analisi matematica.
queste sono proporzionalità inverse. Per cui, visto che -8/3 < -2, allora semplicemente capisci che inizialmente prevale la funzione che ha per esponente il numero minore(la radiazione), poi prevale quella con esponente maggiore (la materia).
-
Allegati: 2
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
@Enrico Corsaro
In un libro ho trovato la seguente spiegazione Allegato 12584 Allegato 12585 (si tratta della stessa pagina, i segni in blu a fianco indicano il paragrafo importante. Ho dovuto fare due fotografie perchè in una non si leggeva niente).
Mi sembrano un po diverse le funzioni della densità di radiazione e di materia che danno su questo libro rispetto quelle di cui avete parlato tu e Cyg X-1.
Riesci a spiegare per favore?
Il libro è "Introduzione all astrofisica nucleare" di Vittorio Castellani (cattedra di astrofisica di Roma). Ti avverto che il libro è vecchiotto. Risale forse agli anni ottanta quindi forse oggi si usa una funzione diversa per descrivere evoluzione di radiazione e materia.
Però vedo anche che tu inserisci le proporzionalità a^-3 (per la materia) e a^-4 (per la radiazione) nella variazione del fattore di scala t^-2/3, mentre qui non lo fa!
Forse la differenza è che come fai tu descrivi una evoluzione delle componenti facendo un integrale, mentre nel libro semplicemente ricava il valore per un tempo preciso ma senza fare un grafico dell evoluzione nel tempo dei componenti.
Tu che ne dici? Ho interpretato bene?
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Ciao Gaetano. Mi sembra che DarknessLight abbia già dato delle indicazioni.
Provo a darti la mia versione. Se sbaglio, Enrico penserà alle correzioni del caso.
Posso dirti che forse sbagli nel visualizzare la CMB. Mi pare che tu la equipari ad una luce emessa in un dato istante della vita dell'universo, da un corpo localizzato in un punto; quella radiazione ci raggiunge effettivamente dopo un tempo T che dipende dalla distanza dell'oggetto nell'istante dell'emissione e dalla velocità di espansione dell'universo.
Nel caso della CMB le cose vanno diversamente. Questa radiazione è sempre stata intimamente connessa a tutto l'universo. Anche quando l'universo aveva un'età inferiore a 380.000 anni la CMB già esisteva e lo permeava completamente. I fotoni non potevano viaggiare liberamente ma già c'erano: diciamo che tutto l'universo era avvolto da una nebbia costituita da protoni ed elettroni che assorbivano e riemettevano in continuazione i fotoni della CMB. Poi, dopo 380.000 anni dal BB, l'universo è diventato trasparente; la CMB è apparsa ovunque ed ha sempre continuato ad essere ovunque. A causa dell'espansione dell'universo è diminuita la frequenza della radiazione che ha comunque continuato a permeare l'universo.
Prova a pensare ad una superficie sferica su cui vaiggiano in tutte le direzioni i fotoni della CMB. Ogni punto della superficie è raggiunto dal suo bravo fotone. La sfera si dilata ed i fotoni continuano ad essere ovunque, anche se ... stirati e quindi meno energetici.
Fino a quando sarà avvertibile? Mah, penso fin quando ci saranno rilevatori abbastanza potenti da rilevare fotoni con temperatura sempre più prossima allo 0 assoluto.
Temo però che per quel tempo le osservazioni saranno affidate a qualcun altro .... :biggrin:
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Non trovo l'articolo di Corsaro, vedo solo i vostri commenti e le sue risposte, mi piacerfebbe anche leggere la parte 1 e 2;)
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Citazione:
Originariamente Scritto da
Morimondo

Non trovo l'articolo di Corsaro, vedo solo i vostri commenti e le sue risposte, mi piacerfebbe anche leggere la parte 1 e 2;)
@Morimondo, li trovi sia all'inizio dell'articolo in questione che QUI e QUI ;).
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Non sto a quotare, l'argomento è ben identificato. Grazie Dark e Cyg, sto riflettendo sulle cose dette. Non mi torna ancora il fatto che comunque un'onda elettromagnetica più che permeare viaggia a velocità "c" e, per esempio, pensando ad una supernova noi ne vediamo l'effetto nell'esatto "spazio-tempo" in cui è avvenuto e per un breve periodo. Aspetterei di sapere cosa ne pensano anche Red ed Enrico.;)
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Un fotone viaggia a velocità c.
La cmb è costituita da una nuvola di fotoni DIFFUSI PER TUTTO IL VOLUME dell universo che viaggiano ognuno a velocità c.
Il fatto che questi fotoni siano diffusi per tutto il volume dell universo rende la cmb una specie di nebbia fatta di radiazione, diffusa in maniera omogenea nel cosmo.
Più guardiamo lontano dalla terra più vediamo l universo primordiale.
Dove l universo è più primordiale la nebbia di fotoni è piu calda e densa.
Qui vicino a noi la nebbia di fotoni è fredda e rarefatta perchè più recente.
La rarefazione che aumenta nel corso del tempo è dovuta all espansione dell universo nonché all aumento del fattore di scala e quindi ad una maggiore diluizione della densità di fotoni ;)
Poi io ho parlato di fotoni ma la radiazione in realtà mi pare contenga anche elettroni e neutrini se non ricordo male...
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
L omogeneità che presenta è dovuta al disaccoppiamento perfettamente omogeneo (quasi) avvenuto 380 000 anni dopo bb tra materia e radiazione. Le anisotropie sono nell ordine dei millesimi di kelvin se non sbaglio!!!
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Citazione:
Originariamente Scritto da
Gaetano M.

Non sto a quotare, l'argomento è ben identificato. Grazie Dark e Cyg, sto riflettendo sulle cose dette. Non mi torna ancora il fatto che comunque un'onda elettromagnetica più che permeare viaggia a velocità "c" e, per esempio, pensando ad una supernova noi ne vediamo l'effetto nell'esatto "spazio-tempo" in cui è avvenuto e per un breve periodo. Aspetterei di sapere cosa ne pensano anche Red ed Enrico.;)
Cerco di rispondere per ordine, così non facciamo confusione. Ritengo che Dark e Cyg ti abbiamo già detto le cose in modo corretto e piuttosto chiaro. Devi in pratica pensare alla CBR come all'universo stesso, a 380 mila anni, proprio perchè essa effettivamente è stata generata da tutto l'Universo (cioè da ogni suo punto) quando aveva quell'età.
C'è anche da dire che la CBR non continua ad essere emessa, ma è stata prodotta solo in quell'epoca, un meccanismo fisico ben preciso quello della ricombinazione che si è verificato solo una volta. Quindi dovresti pensare alla CBR come al tuo fondo cielo, adesso nero perchè trasparente e con una temperatura di 2.7 K, che a quel tempo invece era opaco ed emetteva tutto per intero a 3000 K.
Se non ricordo male c'era un articolo di Zappalà dove spiegava non la CBR in particolare ma il concetto di universalità di un evento cosmico come il big bang e lo confrontava con uno localizzato di una supernova...magari Red ci aiuta a trovarlo ;).
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Citazione:
Originariamente Scritto da
DarknessLight

Poi io ho parlato di fotoni ma la radiazione in realtà mi pare contenga anche elettroni e neutrini se non ricordo male...
No la CBR è esclusivamente fotonica. Altre emissioni come quelle di neutrini sono da localizzare in epoche differenti, in particolare quando i neutrini si sono disaccoppiati dalla materia, a circa 2 secondi di vita dell'Universo. Il cosmic neutrino background costituisce un altro segnale relitto del big bang che si sta cercando di rilevare. Purtroppo è molto difficile perchè si tratterebbe di neutrini a bassissima energia, circa 2 K, e pertanto molto debolmente interagenti con la materia. Se dovessimo riuscire a trovare questo segnale, riusciremmo ad avere una immagine dell'Universo a 2 secondi di vita, il che sarebbe veramente fantastico.
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Citazione:
Originariamente Scritto da
DarknessLight

Le anisotropie sono nell ordine dei millesimi di kelvin se non sbaglio!!!
Un centomillesimo di Kelvin ;), 1/105.
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Citazione:
Originariamente Scritto da
DarknessLight

@
Enrico Corsaro
In un libro ho trovato la seguente spiegazione
Allegato 12584 Allegato 12585 (si tratta della stessa pagina, i segni in blu a fianco indicano il paragrafo importante. Ho dovuto fare due fotografie perchè in una non si leggeva niente).
Tu che ne dici? Ho interpretato bene?
Il libro va benissimo! Le relazioni sono corrette Dark. La T che compare non è il tempo, come nel caso che discutevamo, ma la temperatura! Ti sta facendo vedere che poichè la densità di energia fotonica decresce con la quarta potenza del fattore scala, allora la temperatura della radiazione decresce linearmente con il fattore di scala, utilizzando la legge di Stefan-Boltzmann per cui
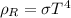
dove T è la temperatura. Quindi il Castellani in quel paragrafo non sta facendo una analisi in termini di tempo ;).
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
@Gaetano M., QUI c'è qualcosa di correlato scritto da Zappalà...ricordo un altro articolo in particolare ma non riesco a trovarlo...
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Citazione:
Originariamente Scritto da
Enrico Corsaro

Il libro va benissimo! Le relazioni sono corrette Dark. La T che compare non è il tempo, come nel caso che discutevamo, ma la temperatura! Ti sta facendo vedere che poichè la densità di energia fotonica decresce con la quarta potenza del fattore scala, allora la temperatura della radiazione decresce linearmente con il fattore di scala, utilizzando la legge di Stefan-Boltzmann per cui
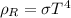
dove T è la temperatura. Quindi il Castellani in quel paragrafo non sta facendo una analisi in termini di tempo ;).
Ok la 1.4 mette in relazione la temperatura della radiazione con l inverso del fattore di scala.
Ma le altre due relazioni (la 1.2 e la 1.3) mi pare proprio che siano come le vostre ovvero la densità di materia proporzionale ad a(t)^-3 e la densità di radiazione(come vedi lui usa il simbolo W) proporzionale ad a(t)^-4.
Solo che lui poi non le inserisce nella variazione del fattore di scala a(t) proporzionale a t^-2/3.
Cioè, così mi pare di capire...:thinking:
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Citazione:
Originariamente Scritto da
DarknessLight

Ok la 1.4 mette in relazione la temperatura della radiazione con l inverso del fattore di scala.
Ma le altre due relazioni (la 1.2 e la 1.3) mi pare proprio che siano come le vostre ovvero la densità di materia proporzionale ad a(t)^-3 e la densità di radiazione proporzionale ad a(t)^-4.
Solo che lui poi non le inserisce nella variazione del fattore di scala t^-2/3.
Cioè, così mi pare di capire...:thinking:
Bravo, esatto ;).
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Citazione:
Originariamente Scritto da
Enrico Corsaro

Cerco di rispondere per ordine, così non facciamo confusione. Ritengo che Dark e Cyg ti abbiamo già detto le cose in modo corretto e piuttosto chiaro. Devi in pratica pensare alla CBR come all'universo stesso, a 380 mila anni, proprio perchè essa effettivamente è stata generata da tutto l'Universo (cioè da ogni suo punto) quando aveva quell'età.
C'è anche da dire che la CBR non continua ad essere emessa, ma è stata prodotta solo in quell'epoca, un meccanismo fisico ben preciso quello della ricombinazione che si è verificato solo una volta. Quindi dovresti pensare alla CBR come al tuo fondo cielo, adesso nero perchè trasparente e con una temperatura di 2.7 K, che a quel tempo invece era opaco ed emetteva tutto per intero a 3000 K.
Se non ricordo male c'era un articolo di Zappalà dove spiegava non la CBR in particolare ma il concetto di universalità di un evento cosmico come il big bang e lo confrontava con uno localizzato di una supernova...magari Red ci aiuta a trovarlo ;).
Penso di essere riuscito a capire aiutato da voi e facendo questo ragionamento che riporto.
380.000 anni dopo il Big Bang l'universo, di cui anche la nostra galassia o quello che era faceva parte, era molto più piccolo. In questo universo si sono formati i fotoni che hanno dato origine alla Radiazione Cosmica di Fondo e che si sono diretti, appena hanno potuto, in tutte le direzioni. Di questi fotoni continuiamo e continueremo a vedere esclusivamente quelli compatibili con la nostra posizione rispetto al loro cono di luce e compatibili con l'espansione dell'universo. Naturalmente stiamo vedendo quello che sono diventati dopo 13,7 miliardi di anni. Aspetto commenti anche cattivi:biggrin:
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Pensate ad un universo senza gravità: sarebbe composto da materia (idrogeno molecolare, protoni, elio cosmologico, ecc..) distribuita in maniera omogenea e diffusa come una nebbia. E guardando lontano da noi vedremmo la materia regredire a stati di densità e temperatura sempre più elevati fino a raggiungere l epoca della ricombinazione dove vedremmo tutta la materia dell universo super concentrata in pochissimo spazio e poi non vedremmo più nulla perché i fotoni sarebbero riassorbiti dalla materia e non ci sarebbe interazione elettromagnetica efficacie.
Lo stesso vale per la cmb. È una nebbia omogenea e diffusa. Noi ne vediamo quella porzione che ci investe in base al suo cono di luce che si interseca con il nostro (questo è ovvio, altrimenti non la vedremmo ;)), quindi vediamo solo quei fotoni della cmb che arrivano alla terra e all occhio dell astronomo, ma questo è logico, come anche della luce del sole ne cogliamo solo una parte.
però la cmb è uniformemente diffusa perchè sono i fotoni che sono stati rilasciati dalla materia NELLO STESSO MOMENTO IN TUTTO IL VOLUME DELL UNIVERSO!!!
E il momento esatto è appunto 380 000 anni dal BB.
Come mi pare dicesse Enrico, dobbiamo pensare alla cmb come se fosse l universo stesso!
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Mi piace la capacita' di sintesi! Grazie Dark, se ogni tanto fai un riassuntino di questo
genere ne giovero' tantissimo, faccio una fatica a starvi dietro! Ma insisto a provarci perche'
son cocciuto :)
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
giusto si,da quel che ho capito io la radiazione cosmica di fondo è stato un lampo nella notte(il primo) e ha permeato tutto il palloncino(ecco perchè si vede dappertutto). poi tutto è tornato buio fino alla formazione della materia diciamo "ordinaria" dove hanno cominciato ad emettere luce gli oggetti singoli (quasar,galassie)
....è corretto?
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Ragazzi non pensavo ci seguiste. Comunque davvero fate le vostre domande!! Magari alcuni chiedono cose più approfondite ma è più bello se in tanti partecipano!
Comunque, un riassunto semplice: senza stare a dire cosa sia il Big bang, sappiamo che un tempo tutto l universo (ovvero spazio-tempo, radiazione, materia barionica, energia oscura) era concentrato in un punto molto piccolo. Questa era la singolarità.
Di colpo questo punto inizia ad espandersi molto velocemente, quindi l universo inizia ad AUMENTARE DI VOLUME MOLTO VELOCEMENTE.
All inizio (durante la singolarità) capirete che tutte le componenti dell universo che ho elencato prima, cioè la radiazione (ovvero i fotoni, insomma la luce e tutto lo spettro elettromagnetico), la materia barionica (ovvero gli atomi della tavola periodica e la famosa materia oscura) e l energia oscura (una forza repulsiva di natura ancora sconosciuta), erano tutti concentrati in poco spazio, quindi il loro destino era unito. Ciò significa che la materia (quindi i protoni, i neutroni, i primi nuclei atomici come H2 ed He) erano strettamente interconnessi alla radiazione elettromagnetica.
Insomma i fotoni (la luce) venivano assorbiti dalla materia che li rilasciata poco dopo, ma poiché lo spazio era poco e tutto era concentrato in poco spazio, allora appena la materia rilasciava radiazione (emissione), la radiazione veniva subito riassorbita da altra materia.
Tutto era appiccicato ed era difficile fare una distinzione tra le varie componenti dell universo.
Pensate che l universo era quindi completamente saturo di materia e radiazione che erano ovunque e non c era spazio vuoto come c è oggi. Quindi era tutto appiccicato, radiazione e materia erano unite tra loro, così visto che la radiazione non poteva essere emessa noi non possiamo vedere nulla: ricordate che la radiazione è anche la luce che ci permette di vedere.
ad un certo punto, con l espansione dello spazio di cui parlavo prima, la radiazione e la materia hanno avuto sufficiente spazio per evolvere seguendo destini separati.
così i fotoni (radiazione) emessa dalla materia non venivano più riassorbiti subito dopo da altra materia, perchè adesso avevano più spazio disponibile per muoversi ed iniziavano a crearsi dei vuoti tra un aggregato di materia ed un altro.
Questa è detta RICOMBINAZIONE, avvenuta 380 000 anni dopo il Big bang e rappresenta appunto la separazione tra materia e radiazione.
La cmb di cui stiamo parlando è il resto fossile di questo evento. Insomma, una prova del Big bang.
ovviamente visto che la materia e la radiazione erano diffuse in maniera omogenea nell universo primordiale, anche l emissione della radiazione è stata omogenea, ed infatti oggi percepiamo la cmb (ovvero la radiazione rilasciata 380 000 anni dopo il Big bang) così perfettamente omogenea.
Spero di avervi aiutato ;)
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Ho finito i grazie! Quindi grazie!
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Citazione:
Originariamente Scritto da
Gaetano M.

Penso di essere riuscito a capire aiutato da voi e facendo questo ragionamento che riporto.
380.000 anni dopo il Big Bang l'universo, di cui anche la nostra galassia o quello che era faceva parte, era molto più piccolo. In questo universo si sono formati i fotoni che hanno dato origine alla Radiazione Cosmica di Fondo e che si sono diretti, appena hanno potuto, in tutte le direzioni. Di questi fotoni continuiamo e continueremo a vedere esclusivamente quelli compatibili con la nostra posizione rispetto al loro cono di luce e compatibili con l'espansione dell'universo. Naturalmente stiamo vedendo quello che sono diventati dopo 13,7 miliardi di anni. Aspetto commenti anche cattivi:biggrin:
In un certo senso il "cono di luce" della CBR ingloba tutto ciò che possiamo vedere noi, poichè è un evento avvenuto dopo l'inflazione e perchè è accaduto in ogni punto dell'Universo. Il cono di luce ha propriamente senso se definito per un singolo osservatore e nel qual caso è meglio dire che è il nostro cono di luce passato a ricevere tutto il segnale della CBR, ovunque essa si sia originata e da ogni punto.
Comunque mi pare che ci siamo Gaetano, ottimo così e ottimo anche per tutti gli altri partecipanti che rendono queste discussioni ancora più belle ed interessanti, continuate così!
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
@Marcos64, ovviamente siamo qui proprio per farci capire per cui è essenziale anzi che se qualcosa non ti è chiara ci chiedi e si cerca di discuterla insieme ;).
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Ti volevo chiedere Enrico, se è noto il momento (in termini di età dell'universo) in cui si è avuto il "pareggio" tra densità della radiazione e della materia. Ho pensato, forse troppo semplicisticamente, che uguagliando le due equazioni che rendono le due densità in questione, noto il tempo, si potrebbe ricavare almeno il rapporto tra le due costanti di proporzionalità che legano le densità al tempo.
Naturalmente mi aspetto che le costanti di proporzionalità varino - non con il tempo - ma con altre caratteristiche della materia e della radiazione; ad esempio il fatto che la materia sia andata organizzandosi in modo molto diverso al trascorrere del tempo (dalle particelle iniziali che costituivano un plasma all'organizzazione attuale in ammassi di galassie) immagino influisca sul valore della sua costante.
Diciam0 allora che il mio tentativo è destinato a fallire, ma ..... almeno il periodo in cui si è avuto il "pareggio" è noto?
A proposito dell'equazione di stato cosmologica, ti chiedo se la densità che vi compare è quella totale (materia "normale" e radiazione, escluse materia ed energia oscure?). Allora p è la pressione esercitata dalle stesse grandezze che compaiono nelle densità?
Ti posso chiedere su quali ipotesi si basa la forma dell'equazione di stato? Ad occhio e croce mi sembra abbastanza lontana da quella dei gas perfetti che si studia a scuola.
Scusami se ti bombardo con le domande, ma la curiosità è tanta .....
-
Allegati: 1
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
@Cyg X-1
Citazione:
è noto il momento (in termini di età dell'universo) in cui si è avuto il "pareggio" tra densità della radiazione e della materia?
Guarda qui
Allegato 12626
Trovi la spiegazione del grafico nella parte I degli articoli di Enrico. Qui come vedi il momento di "pareggio" lo dà in funzione della T e non del tempo, però almeno aiuta a chiarirsi le idee ;)
(La linea retta orizzontale è l energia oscura)
-
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Citazione:
Originariamente Scritto da
Cyg X-1

Ti volevo chiedere Enrico, se è noto il momento (in termini di età dell'universo) in cui si è avuto il "pareggio" tra densità della radiazione e della materia. Ho pensato, forse troppo semplicisticamente, che uguagliando le due equazioni che rendono le due densità in questione, noto il tempo, si potrebbe ricavare almeno il rapporto tra le due costanti di proporzionalità che legano le densità al tempo.
Si, l'approccio è corretto sostanzialmente. Mettendo a sistema le due relazioni che mostrano la dipendenza della densità di energia nei due casi rispetto al tempo, trovi il valore di tempo per cui si eguagliano, cioè
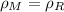
Il grafico che ti ha ben inserito Dark ti mostra già il discorso e ti fornisce anche i valori in termini di temperatura.
Sfruttando la relazione che citavamo nei post precedenti, puoi convertire la temperatura in un tempo di evoluzione dell'Universo. Semplicemente perchè
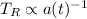
e quindi per la radiazione essendo
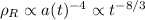
trovi che 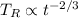
In parole povere, la temperatura della radiazione è direttamente legata al tempo di vita dell'Universo e ne descresce come una potenza elevata a 2/3.
Nel grafico ti mostra che il punto che corrisponde a Log T = 0, cioè ad una temperatura pari a 1 eV (considerata come kT, dove k è la costante di Boltzmann), è avvenuta l'uguaglianza tra materia e radiazione.
Citazione:
Originariamente Scritto da
Cyg X-1

Naturalmente mi aspetto che le costanti di proporzionalità varino - non con il tempo - ma con altre caratteristiche della materia e della radiazione; ad esempio il fatto che la materia sia andata organizzandosi in modo molto diverso al trascorrere del tempo (dalle particelle iniziali che costituivano un plasma all'organizzazione attuale in ammassi di galassie) immagino influisca sul valore della sua costante.
Diciam0 allora che il mio tentativo è destinato a fallire, ma ..... almeno il periodo in cui si è avuto il "pareggio" è noto?
In realtà le costanti di porporzionalità sarebbero una costante sola, unica sia per materia che per radiazione, almeno fino all'epoca in cui esse erano accoppiate poichè dominava la radiazione. Quindi il periodo a cui facciamo riferimento è grossomodo corrispondente a 350 mila anni dopo il Big Bang.
Citazione:
Originariamente Scritto da
Cyg X-1

A proposito dell'equazione di stato cosmologica, ti chiedo se la densità che vi compare è quella totale (materia "normale" e radiazione, escluse materia ed energia oscure?). Allora p è la pressione esercitata dalle stesse grandezze che compaiono nelle densità?
Ti posso chiedere su quali ipotesi si basa la forma dell'equazione di stato? Ad occhio e croce mi sembra abbastanza lontana da quella dei gas perfetti che si studia a scuola.
L'equazione di stato cosmologica si riferisce alla densità di energia in generale in qualsiasi forma (non materia in particolare ma energia di qualsiasi costituente, che sia dunque radiazione, materia o energia oscura), e della pressione totale.
In realtà è molto simile all'equazione di stato di un gas perfetto nel caso della materia, che vedo di ricavarti qui per capirci subito.
La legge del gas perfetto deriva da quella di un gas ideale, data come
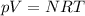
dove p è la pressione, V il volume, N il numero di moli, R la costante del gas ideale, T la temperatura.
Per un gas perfetto hai una versione semplificata dovuta al fatto che puoi trascurare le forze intermolecolari. Avrai che
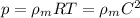
dove \rho_m è la densità di materia (da non confondere con la precedente 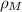 che invece è la densità di energia associata a materia) e C è una velocità termica caratteristica delle molecole, data da
che invece è la densità di energia associata a materia) e C è una velocità termica caratteristica delle molecole, data da 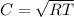 .
.
Adesso passando da 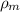 densità di materia, a
densità di materia, a 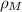 la densità di energia dovuta a materia, hai che
la densità di energia dovuta a materia, hai che 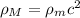 , dove c è la velocità delle onde e.m., per la legge di equivalenza tra energia e materia.
, dove c è la velocità delle onde e.m., per la legge di equivalenza tra energia e materia.
L'equazione di prima dunque diventa nel caso dell'energia di materia
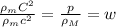
dove w è il fattore dell'equazione di stato cosmologica ed è pari a zero in questo caso specifico.
Quindi ricapitolando, partendo dall'espressione generale dell'equazione di stato cosmologica avrai
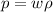
dove 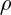 è una densità di energia. A seconda del tipo di energia che consideri, avrai la corrispettiva equazione di stato. Se l'energia che consideri è quella della materia, l'equazione di stato cosmologica diventa l'equazione dei gas perfetti, come ti ho mostrato.
è una densità di energia. A seconda del tipo di energia che consideri, avrai la corrispettiva equazione di stato. Se l'energia che consideri è quella della materia, l'equazione di stato cosmologica diventa l'equazione dei gas perfetti, come ti ho mostrato.


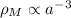
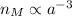
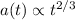
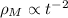
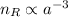
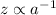
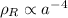
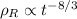
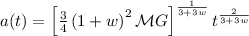
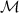 è la quantità totale di materia nell'Universo, G la costante di gravitazione universale, e il coefficiente dell'equazione di stato cosmologica
è la quantità totale di materia nell'Universo, G la costante di gravitazione universale, e il coefficiente dell'equazione di stato cosmologica 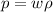 , pari a w = 0 per un Universo dominato da polveri, w = 1/3 se dominato da radiazione, w = 1 per Stiff matter, cioè materia rigida, come quella di un Universo primordiale estremamente denso.
, pari a w = 0 per un Universo dominato da polveri, w = 1/3 se dominato da radiazione, w = 1 per Stiff matter, cioè materia rigida, come quella di un Universo primordiale estremamente denso.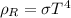
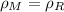
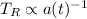
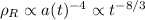
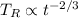
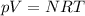
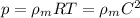
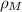 che invece è la densità di energia associata a materia) e C è una velocità termica caratteristica delle molecole, data da
che invece è la densità di energia associata a materia) e C è una velocità termica caratteristica delle molecole, data da 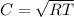 .
.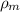 densità di materia, a
densità di materia, a 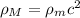 , dove c è la velocità delle onde e.m., per la legge di equivalenza tra energia e materia.
, dove c è la velocità delle onde e.m., per la legge di equivalenza tra energia e materia.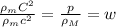
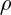 è una densità di energia. A seconda del tipo di energia che consideri, avrai la corrispettiva equazione di stato. Se l'energia che consideri è quella della materia, l'equazione di stato cosmologica diventa l'equazione dei gas perfetti, come ti ho mostrato.
è una densità di energia. A seconda del tipo di energia che consideri, avrai la corrispettiva equazione di stato. Se l'energia che consideri è quella della materia, l'equazione di stato cosmologica diventa l'equazione dei gas perfetti, come ti ho mostrato.