Re: Geometria dell'universo
Per quanto riguarda la superficie sferica di raggio  dobbiamo fare un po' pi¨ di conti.. :razz:
dobbiamo fare un po' pi¨ di conti.. :razz:
Notazione e premessa:
- La virgola negli indici indica la derivata, per esempio
- Consideriamo ora una metrica tempo indipendente, quindi avremo solo due coordinate:
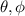 .
.
Partiamo dalla metrica:
Ricordiamo la definizione dello scalare di Ricci 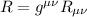 dove
dove 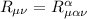 Ŕ la contrazione del tensore di Riemann. Il tensore di Riemann a sua volta Ŕ definito come dove gamma sono i simboli di Christoffel Gli unici simboli di Christoffel non nulli saranno
Ŕ la contrazione del tensore di Riemann. Il tensore di Riemann a sua volta Ŕ definito come dove gamma sono i simboli di Christoffel Gli unici simboli di Christoffel non nulli saranno 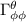 e
e 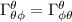 .
.
Ora abbiamo tutto! Basta "solamente" tanta voglia di fare conti e derivate, per˛ in maniera molto lineare si pu˛ calcolare il valore del tensore di Riemann, farne la contrazione del primo e terzo indice ottenendo il tensore di Ricci e ulteriormente contrarre questo per ottenere lo scalare di Ricci.
Ovviamente questi conti sono lunghissimi. Conviene sfruttare una proprietÓ fondamentale dello spaziotempo. Preso un qualunque punto P in ogni spaziotempo, Ŕ possibile scegliere un sistema di coordinate tale che la metrica sia quella di Minkowski. Questo sistema viene detto Local Inertial Frame (LIF). In questo modo, se riusciamo a trovare un punto in cui 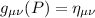 e
e 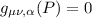 , i conti si semplificano di molto! Infatti lo scalare di Ricci assume la forma:
, i conti si semplificano di molto! Infatti lo scalare di Ricci assume la forma:
╚ possibile costruire al polo nord della sfera un sistema di coordinate che soddisfi le condizioni dette poco fa: al polo Ŕ quindi possibile costruire un LIF semplificando i conti. La metrica quindi in prossimitÓ del polo nord vale
Sembra molto pi¨ complessa ma, esattamente al polo (con x=0 e y=0) questa diventa l'identitÓ 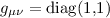 . Calcoliamo R con la (4) sommando su tutti gli indici:
. Calcoliamo R con la (4) sommando su tutti gli indici:
Molti termini si annullano e giungiamo alla forma
Le derivate seconde della metrica valgono
Possiamo finalmente concludere facendo questa ultima somma:
Ed eccoci al risultato! La curvatura di una sfera di raggio  vale
vale 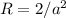 al polo nord. Ora, dato che la sfera Ŕ simmetrica, la curvatura al polo nord sarÓ la stessa in ogni altro punto sulla superficie sferica!
al polo nord. Ora, dato che la sfera Ŕ simmetrica, la curvatura al polo nord sarÓ la stessa in ogni altro punto sulla superficie sferica!
dobbiamo fare un po' pi¨ di conti.. :razz:
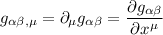
.
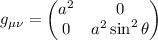
dove
Ŕ la contrazione del tensore di Riemann. Il tensore di Riemann a sua volta Ŕ definito come
dove gamma sono i simboli di Christoffel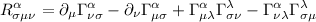 Gli unici simboli di Christoffel non nulli saranno
Gli unici simboli di Christoffel non nulli saranno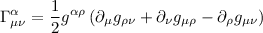
e
.
e
, i conti si semplificano di molto! Infatti lo scalare di Ricci assume la forma:
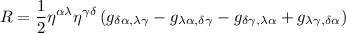
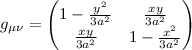
. Calcoliamo R con la (4) sommando su tutti gli indici:
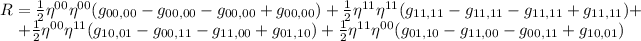
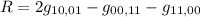
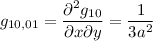
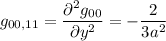
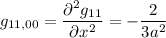
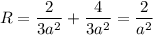
vale
al polo nord. Ora, dato che la sfera Ŕ simmetrica, la curvatura al polo nord sarÓ la stessa in ogni altro punto sulla superficie sferica!
