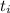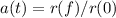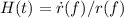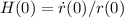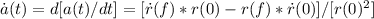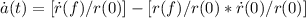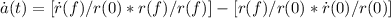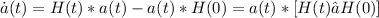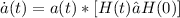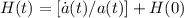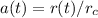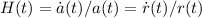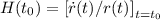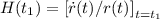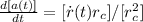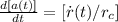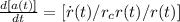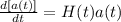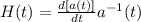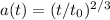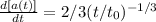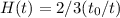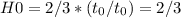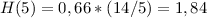Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Voglio ringraziare Dark e, ovviamente, Enrico per le delucidazioni.
Fatemi leggere quanto mi avete inviato. Ce n'è di materia per riflettere!!!
Questa cavalcata di cosmologia promette di essere davvero istruttiva. Perchè non ... allungarla un pò affrontando tutte le più importanti tematiche della cosmologia legate al MS?
Potrebbe diventare una sorta di tutorial, sempre che Enrico non l'avesse già pensata in questi termini ...
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Certo tutto è possibile ;), procediamo piano piano in modo anche da dare il tempo a più lettori di assimilare l'argomento. La parte successiva alle III sarà relativa al modo in cui si usa la CBR per vincolare i parametri del modello standard...sono abbastanza certo che l'argomento vi risulterà interessante, anche perchè è abbastanza ingegnoso e c'è molta fisica in mezzo.
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Ciao Enrico e ciao a tutti.
Mi scuso fin da subito per quanto leggerete in questo mio commento. Non ho alcuna intenzione di rifondare la cosmologia!
Il fatto è che non ho mai trovato una ipotetica legge di variazione del parametro di Hubble con il tempo. Allora ho cominciato a cercare di capire se, con le equazioni a disposizione, si potesse arrivare a qualche interessante conclusione.
Ho quindi elaborato i calcoli che vedete di seguito; i passaggi matematici sono abbastanza semplici.
Chiedo ad Enrico la fatica supplementare di raccapezzarsi nel guazzabuglio per darmi del … matto oppure intravedere un barlume di lucidità nel mio sproloquio ….
Bene, parto.
Un qualunque oggetto celeste può essere considerato secondo tre diverse modalità:
- La sua apparenza osservata, nell’istante in cui la sua luce raggiunge l’occhio dell’osservatore. Ho indicato con (f) questa modalità.
- La sua consistenza al tempo in cui la sua luce fu emessa, tempo antecedente a quello di osservazione. Ho indicato con (t) questa modalità.
- La sua consistenza al tempo attuale, non osservabile, poiché la luce emessa in questo momento ha appena lasciato l’oggetto e non ha certo potuto raggiungerci. La distanza dell’oggetto ad oggi è chiamata distanza comovente. Ho indicato con © questa modalità.
Sappiamo che il fattore di scala a(t) dell’universo è definito come:
a(t) = r(f)/r©
dove:
- a(t) è il fattore di scala attribuito all’universo al generico tempo t (età dell’universo);
- r(f) è la distanza tra due oggetti, stabilita in base a determinati parametri osservativi (ad esempio, le candele standard);
- r© è la distanza comovente, cioè la distanza tra i due stessi oggetti al tempo presente, stabilita in base al modello di universo adottato.
Il parametro di Hubble H(t) è definito come:
H(t) = ṙ(f)/r(f)
dove:
- H(t) è il parametro di Hubble, funzione del tempo t (età dell’universo);
- r(f) è, di nuovo, la distanza tra due oggetti stabilita in base a determinati parametri osservativi (ad esempio, le candele standard);
- ṙ(f) rappresenta la variazione di detta distanza rispetto al tempo, cioè la derivata rispetto al tempo.
La costante di Hubble H© è definita come:
H© = ṙ©/r©
dove:
- H© è la costante di Hubble, cioè il valore del parametro di Hubble al tempo presente;
- ṙ© è la velocità di recessione tra due oggetti, al tempo presente;
- r© è la distanza tra i due stessi oggetti al tempo presente (distanza comovente).
A questo punto scrivo:
ả(t) = d[a(t)/dt] = [ṙ(f)*r© - r(f)*ṙ©]/[r©^2] =
[ṙ(f)/r©] - [r(f)/r© * ṙ©/r©] =
[ṙ(f)/r© * r(f)/r(f)] - [r(f)/r© * ṙ©/r©] =
H(t)*a(t) - a(t)*H© = a(t)*[H(t) - H©] =
Ottengo infine:
ả(t) = a(t) * [H(t) - H©]
da cui, finalmente:
H(t) = [ả(t)/a(t)] + H©
Applico l’espressione al caso di un universo piatto fin dalla sua origine. Per detto universo vale la relazione:
a(t) = r(f)/r© = (t/t© )^2/3
ả(t) = H(t)*a(t) - a(t)*H© = a(t)*[H(t) - H©]
= [2*t^(-1/3)]/[3* t©^(2/3)]
da cui:
H(t) = H© + ṙ(f)/r(f) = [2/(3*t)] + H©
Si vede come, ponendo H©=70 km/(s*Mpc), occorra un tempo infinito perché H(t) assuma detto valore. Un universo piatto fin dall’origine impiegherebbe un tempo lunghissimo per veder diminuire H(t) ai valori oggi osservati, dopo “soli” 14 miliardi di anni.
Allora, per rendere i nostri calcoli aderenti all’universo osservato, dobbiamo definire il parametro H© dell’equazione, in modo tale che sia: H(14) = 0,0715 mld anni^-1.
Si tratta del valore accreditato alla costante di Hubble, pari a 70 km/(s*Mpc).
Fissate le condizioni al contorno, calcolo quindi il valore del parametro H©:
H(14) = 0,0715 = [2/(3*14)] + H©
da cui:
H© = 0,0238 mld anni^-1
A questo punto dovrei poter ricavare il valore del parametro di Hubble per qualunque età dell’universo (t), sfruttando l’equazione:
H(t) = [2/(3*t)] + 0,0238
H(1) = 0,690 [mld anni^-1] = 675 [km/(s*Mpc]
H(2) = 0,357 [mld anni^-1] = 349 [km/(s*Mpc]
H(3) = 0,246 [mld anni^-1] = 241 [km/(s*Mpc]
H(4) = 0,190 [mld anni^-1] = 186 [km/(s*Mpc]
H(5) = 0,157 [mld anni^-1] = 154 [km/(s*Mpc]
H(6) = 0,135 [mld anni^-1] = 132 [km/(s*Mpc]
H(7) = 0,119 [mld anni^-1] = 116 [km/(s*Mpc]
H(8) = 0,107 [mld anni^-1] = 105 [km/(s*Mpc]
H(9) = 0,098 [mld anni^-1] = 96 [km/(s*Mpc]
H(10) = 0,090 [mld anni^-1] = 88 [km/(s*Mpc]
H(11) = 0,084 [mld anni^-1] = 82 [km/(s*Mpc]
H(12) = 0,079 [mld anni^-1] = 77 [km/(s*Mpc]
H(13) = 0,075 [mld anni^-1] = 73 [km/(s*Mpc]
H(14) = 0,071 [mld anni^-1] = 70 [km/(s*Mpc]
Ovviamente la storia dell’universo è ben più tormentata di quanto sia insito nell’ipotesi semplificatrice di un cosmo piatto fin dall’origine.
A conclusione, chiedo ad Enrico se ha un qualche grafico che mostri l’andamento di H(t) con l’età del cosmo.
Grazie e scusate ancora.
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
@Cyg X-1 ti posso chiedere una cortesia?
Abbiamo inserito un sistema di scrittura equazioni con LaTeX.
Lo puoi usare con il comando [MAT] che hai nel menu sopra.
Puoi per favore riscrivere le tue equazioni con questo formato? Abbi pazienza però con i simboli in quel modo mi viene piuttosto confusionario seguirti.
Per capire come usare questa funzionalità dai una occhiata QUI. Sarà molto molto più semplice anche per chi ci legge seguire il discorso.
Nell'eventualità, per una prossima volta ti consiglio di dividere il post in due parti, così che si ha una visione migliore del problema e si può rispondere per gradi, soprattutto se metti così tanti numeri in mezzo.
Ti ringrazio per la comprensione! ;)
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Aspetta frena un attimo...Cerchiamo prima di tutto di fare un pò di chiarezza. Ti conviene fare le prove nello stesso post che ti ho linkato sulla nuova funzionalità, non qui altrimenti ci confondiamo tutti. Ti cancello gli ultimi post per evitare problemi.
Un paio di consigli:
1) Perchè usare il simbolo di copyright? Basta mettere un pedice zero, per i valori di riferimento.
2) Non usare simboli diversi per parlare di quantitià fisiche uguali. Se usi t per il tempo, continua ad usare t e non f. Invece di chiamarlo f, chiamalo 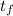 , mentre t iniziale lo puoi chiamare
, mentre t iniziale lo puoi chiamare 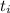
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Ho cercato di seguire i tuoi consigli. Pubblico, per il momento, solo la prima parte.
La differenza tra i pedici t e f l'ho indicata qui sotto, quindi li lascerei immutati.
Speriamo che ora il commento si legga correttamente, altrimenti non so cosa fare ....
Un qualunque oggetto celeste può essere considerato secondo tre diverse modalità:
- La sua apparenza osservata, nell’istante in cui la sua luce raggiunge l’occhio dell’osservatore. Ho indicato con (f) questa modalità.
- La sua consistenza al tempo in cui la sua luce fu emessa, tempo antecedente a quello di osservazione. Ho indicato con (t) questa modalità.
- La sua consistenza al tempo attuale, non osservabile, poiché la luce emessa in questo momento ha appena lasciato l’oggetto e non ha certo potuto raggiungerci. La distanza dell’oggetto ad oggi è chiamata distanza comovente. Ho indicato con (0) questa modalità.
Sappiamo che il fattore di scala a(t) dell’universo è definito come:
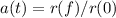
dove:
- a(t) è il fattore di scala attribuito all’universo al generico tempo t (età dell’universo);
- r(f) è la distanza tra due oggetti, stabilita in base a determinati parametri osservativi (ad esempio, le candele standard);
- r(0) è la distanza comovente, cioè la distanza tra i due stessi oggetti al tempo presente, stabilita in base al modello di universo adottato.
Il parametro di Hubble H(t) è definito come:
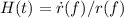
dove:
- H(t) è il parametro di Hubble, funzione del tempo t (età dell’universo);
- r(f) è, di nuovo, la distanza tra due oggetti stabilita in base a determinati parametri osservativi (ad esempio, le candele standard);
- \dot{r}(f) rappresenta la variazione di detta distanza rispetto al tempo, cioè la derivata rispetto al tempo.
La costante di Hubble H(0) è definita come:
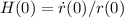
dove:
- H(0) è la costante di Hubble, cioè il valore del parametro di Hubble al tempo presente;
- \dot{r}(0) è la velocità di recessione tra due oggetti, al tempo presente;
- r(0) è la distanza tra i due stessi oggetti al tempo presente (distanza comovente).
A questo punto scrivo:
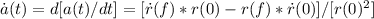
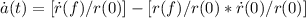
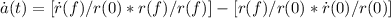
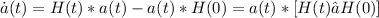
Ottengo infine:
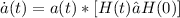
da cui, finalmente:
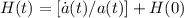
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Macchè si è mangiato tutti gli apici delle derivate rispetto al tempo.
Vabbè, scusate, ci ho provato .... si vede che non è aria, pazienza.
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Citazione:
Originariamente Scritto da
Cyg X-1

Macchè si è mangiato tutti gli apici delle derivate rispetto al tempo.
Vabbè, scusate, ci ho provato .... si vede che non è aria, pazienza.
Niente panico...ti ho sistemato le derivate con i puntini, usando il comando \dot{}.
Due cose alla base secondo me non vanno bene.
1) non capisco cosa intendi dire con apparenza e consistenza dell'oggetto. Se ti riferisci al segnale elettromagnetico che giunge a noi, allora parlerei semplicemente di tempo in cui il segnale è stato emesso e tempo in cui è arrivato a noi. Dato che stiamo parlando di posizioni nello spazio e nel tempo, le uniche quantità che entrano in gioco sono distanze e tempo stesso, oltre alle relative velocità che hai riportato.
2) La definizione di fattore scala a(t) è sbagliata così come la riporti. Non va bene definire un fattore di scala in funzione di t ed esprimerlo come il rapporto di una distanza espressa con il simbolo f. E' come se stessi confrontando mele con arance, l'uno non è l'altro.
Dobbiamo risistemare un pò il formalismo, perchè i simboli tra parentesi tonde indicano esplicitamente dipendenze funzionali, e non sono da utilizzare come simboli di diversificazione.
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Citazione:
Originariamente Scritto da
Cyg X-1

Un qualunque oggetto celeste può essere considerato secondo tre diverse modalità:
- La sua apparenza osservata, nell’istante in cui la sua luce raggiunge l’occhio dell’osservatore. Ho indicato con (f) questa modalità.
- La sua consistenza al tempo in cui la sua luce fu emessa, tempo antecedente a quello di osservazione. Ho indicato con (t) questa modalità.
- La sua consistenza al tempo attuale, non osservabile, poiché la luce emessa in questo momento ha appena lasciato l’oggetto e non ha certo potuto raggiungerci. La distanza dell’oggetto ad oggi è chiamata distanza comovente. Ho indicato con (0) questa modalità.
Sostituirei queste definizioni con le seguenti:
- Il generico istante di tempo lo indichiamo con t
- L'istante in cui il segnale elettromagnetico emesso dalla sorgente giunge a noi lo indichiamo con t0 (istante attuale)
- L'istante in cui il segnale elettromagnetico viene emesso dalla sorgente lo indichiamo con t1 (tempo iniziale)
Per le distanze invece:
- La distanza che ha l'oggetto ad un tempo generico, indicata come r(t)
- La distanza che ha la sorgente quando emette il segnale, r(t1) = r1
- La distanza che ha la sorgente quando invece riceviamo il segnale, r(t0) = r0
- La distanza comovente dell'oggetto, indicata come rc (per non confonderla con le altre che invece dipendono dal tempo)
Fatte queste definizioni si può procedere a riscrivere le equazioni. Il fattore di scala diventa dunque al tempo generico t
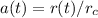
come è intuitivamente ottenibile.
La costante di Hubble per un qualsiasi istante t di tempo diventa, dalla definizione
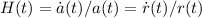
Chiaramente per il tempo attuale avremo che
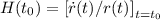
dove ho messo che la quantità al secondo membro è calcolata per l'istante t = t0 cioè il tempo attuale in cui riceviamo il segnale. Per semplicità possiamo chiamare H(t0) = H0.
Per il tempo in cui invece viene emesso il segnale dalla sorgente avremo
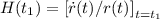
Ci siamo fin qui?
A questo punto hai sostanzialmente realizzato la derivata del fattore di scala partendo dalla sua definizione ma hai messo in mezzo un errore concettuale "grave", cioè che la coordinata comovente dipende dal tempo (che tu hai indicato con r(0) ). La coordinata comovente non dipende dal tempo e per questo non è derivabile rispetto al tempo, ma risulta come un fattore costante. Hai implicitamente fatto questa operazione (correttamente tra l'altro) quando hai espresso la costante di Hubble prima in termini di a(t) e poi in termini di r(t).
Quindi purtroppo le equazioni che riporti alla fine sono tutte sbagliate.
Fammi sapere se la cosa ti è chiara ;).
Re: Il modello cosmologico standard ΛCDM - Parte III: storia e proprietà della CBR
Si, sono d’accordo con quanto hai scritto e concordo pienamente sulla gravità dell’errore commesso nel derivare la distanza comovente, che è costante.
Allora riprendo la mia espressione annullando la derivata in questione. Vediamo cosa succede:
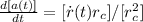
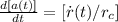
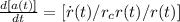
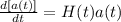
da cui:
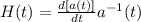
Ora mi prendo la definizione di fattore di scala per un universo piatto:
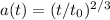
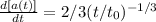
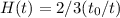
Se pongo t=t0 (tempo attuale) dovrei ricavare H0:
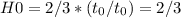
Ma questo valore cosa significa?
D’altra parte, se ad esempio pongo t=5, dovrei ottenere:
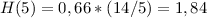
Quindi il parametro di Hubble nel momento in cui l’universo aveva 5 miliardi di anni valeva 1,84/0,66=2,8 volte il valore attuale, e cioè 2,8*70=196 km/(s*Mpc)?

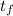 , mentre t iniziale lo puoi chiamare
, mentre t iniziale lo puoi chiamare