Ricavare le equazioni di Einstein

[mazzolatore]

Ciao a tutti il post di @manzonis, sulle geodediche mi ha ispirato a dare una riletta a qualche appunto di relatività generale, allora cercherò di collegarmi al suo discorso per arrivare alla/e famosissima equazione di Einstein.

Per non ripercorrere tutta la matematica e iniziare da troppo lontano, partiamo da alcune conoscenze ottenute preliminarmente, cioè dal tensore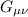
Un tensore come questo in matematica può essere visualizzato come una matrice i cui indici possono variare, se abbiamo 3 indici il tensore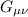 sarà una matrice 3x3, se sono 4 una matrice 4x4, tali indici rappresentano le coordinate e visto che siamo in relatività le coordinate sono 4 (3 spaziali e 1 temporale)

1-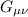 è un tensore;
2-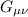 è lineare nelle derivate seconde, e quadratico nelle derivate prime della metrica;
3-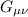 è simmetrico;
4-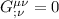 la Divergenza covariante è nulla
5-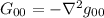

La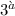 proprietà ci dice che la matrice che rappresenta il tensore è simmetrica, volgarmente tale matrice è specchiata rispetto la diagonale
mentre la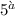 si ricollega al discorso che faceva @manzonis, ovvero sotto le ipotesi di campo stazionario e basse velocità, la fisica relativistica si deve ricollegare alla fisica classica.
Mentre la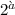 , ci dice una proprietà algebrica che deve soddisfare tale tensore.
Come nel precedente post si vede che il tensore di Riemann è collegato ai simboli di Christoffel, i quali sono legati alla metrica.
Ora si può dimostrare che pochi sono i tensori che si possono costruire lineari nelle derivate seconde della metrica, e quadratici nelle derivate prime.
Questi tensori sono 3;
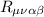Tensore di Riemann
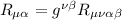Tensore di Ricci
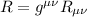Scalare di curvatura

Il tensore di Riemann non va bene, perchè ha 4 indici quindi lo possiamo immaginare come una matrice in 4D, il tensore di Ricci va bene, e come visto, deriva dal tensore di Riemann tramite quella "moltiplicazione" (detta contrazione)* lo scalare di curvatura è un numero, non un tensore, ma possiamo farlo diventare un tensore di rango 2 ().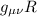
Allora il nostro tensore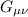 che deve essere lineare nelle derivate seconde e quadratico nelle prime, lo posso scrivere come combinazione lineare, del tensore di ricci e dello scalare di curvatura (che per ipotesi sono lineari nelle derivate seconde e quadratico nelle prime).
Allora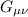 avrà questo aspetto:


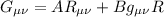
dove A e B sono dei semplici numeri da determinare.
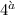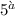Bisogna ancora applicare la e ipotesi.
Usando la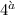 cosa possiamo ricavare?
Basta calcolare la divergenza covariante di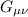 e imporla = 0
Facciamolo.
Ora la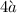 condizione però ha gli indici in alto 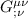mentre il nostro 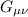li ha bassi, si può facilmente dimostrare che posso alzare e abbassare gli indici (IN QUESTO CASO) senza problemi, quindi;


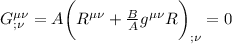
Adesso invece di proseguire in questo calcolo usiamo una famosa identità (identità di bianchi):



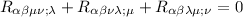
Contraiamo questa espressione con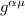 per ogni singolo elemento dentro la parentesi
cioè:



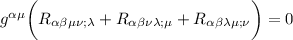
iniziamo dal primo
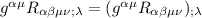, ho portato 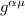dentro la derivata covariante e lo posso fare perche la derivata covariante di 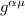è nulla.
Nell'ultima espressione si contraggono 1° e 3° indice e quindi otteniamo:


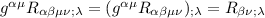
continuiamo con il 3°


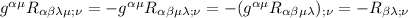
che è lo stesso passaggio di prima, solo che appare quel segno meno, perche nel primo passaggio ho invertito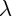 con 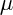e questo comporta la comparsa del segno meno, visto che il tensore di Riemann è antisimmetrico.
Il 2° pezzo lo lasciamo tale e quale, allora arriviamo alla seguente equazione:

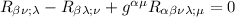
che la contraiamo ulteriormente con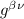

quindi avremo da fare


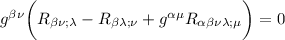
distribuiamo


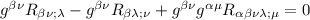
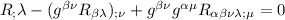
il primo termine si contrae e diventa uno scalare, nel secondo termine ho portato g dentro la derivata covariante come prima, e si contrarrà diventando


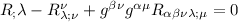
Nell'ultimo pezzo di questa espressione ci lavoriamo un poco sopra, anzitutto commuto le 2 g,

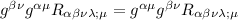
entro nella derivata covariante


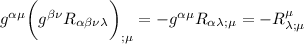
Quindi alla fine l'identità di Bianchi diventa


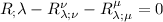
Notare la similitudine dei 2 ultimi termini che sono entrambi derivati in modo covariante per lo stesso indice in altro, allora li sommo (l'indice non è nulla di fisico, in questo caso posso rinominarli) ottenendo;

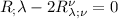
Contraendo con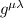 giuro è l'ultima volta
che succede?


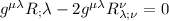
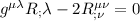
anche qui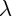 risulta essere indice muto allora lo rinomino in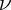


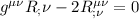
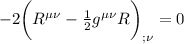
che confrontata con:


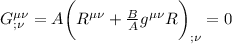
possiamo dire che sono uguali, e abbiamo scoperto che il rapporto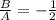

Vedremo come scoprire A nel prossimo post.