Risultati da 1 a 10 di 26
Discussione: Ricavare le equazioni di Einstein
-
17-11-2021, 22:12 #1Nana Bruna


- Data Registrazione
- Jul 2016
- Località
- Cisterna di Latina
- Messaggi
- 271
- Taggato in
- 30 Post(s)


Ricavare le equazioni di Einstein
Ciao a tutti il post di @manzonis, sulle geodediche mi ha ispirato a dare una riletta a qualche appunto di relatività generale, allora cercherò di collegarmi al suo discorso per arrivare alla/e famosissima equazione di Einstein.
Per non ripercorrere tutta la matematica e iniziare da troppo lontano, partiamo da alcune conoscenze ottenute preliminarmente, cioè dal tensore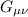
Un tensore come questo in matematica può essere visualizzato come una matrice i cui indici possono variare, se abbiamo 3 indici il tensore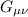 sarà una matrice 3x3, se sono 4 una matrice 4x4, tali indici rappresentano le coordinate e visto che siamo in relatività le coordinate sono 4 (3 spaziali e 1 temporale)
sarà una matrice 3x3, se sono 4 una matrice 4x4, tali indici rappresentano le coordinate e visto che siamo in relatività le coordinate sono 4 (3 spaziali e 1 temporale)
1-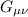 è un tensore;
è un tensore;
2-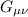 è lineare nelle derivate seconde, e quadratico nelle derivate prime della metrica;
è lineare nelle derivate seconde, e quadratico nelle derivate prime della metrica;
3-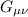 è simmetrico;
è simmetrico;
4-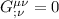 la Divergenza covariante è nulla
la Divergenza covariante è nulla
5-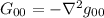
La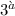 proprietà ci dice che la matrice che rappresenta il tensore è simmetrica, volgarmente tale matrice è specchiata rispetto la diagonale
proprietà ci dice che la matrice che rappresenta il tensore è simmetrica, volgarmente tale matrice è specchiata rispetto la diagonale
mentre la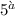 si ricollega al discorso che faceva @manzonis, ovvero sotto le ipotesi di campo stazionario e basse velocità, la fisica relativistica si deve ricollegare alla fisica classica.
si ricollega al discorso che faceva @manzonis, ovvero sotto le ipotesi di campo stazionario e basse velocità, la fisica relativistica si deve ricollegare alla fisica classica.
Mentre la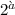 , ci dice una proprietà algebrica che deve soddisfare tale tensore.
, ci dice una proprietà algebrica che deve soddisfare tale tensore.
Come nel precedente post si vede che il tensore di Riemann è collegato ai simboli di Christoffel, i quali sono legati alla metrica.
Ora si può dimostrare che pochi sono i tensori che si possono costruire lineari nelle derivate seconde della metrica, e quadratici nelle derivate prime.
Questi tensori sono 3;
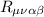 Tensore di Riemann
Tensore di Riemann
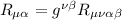 Tensore di Ricci
Tensore di Ricci
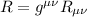 Scalare di curvatura
Scalare di curvatura
Il tensore di Riemann non va bene, perchè ha 4 indici quindi lo possiamo immaginare come una matrice in 4D, il tensore di Ricci va bene, e come visto, deriva dal tensore di Riemann tramite quella "moltiplicazione" (detta contrazione)* lo scalare di curvatura è un numero, non un tensore, ma possiamo farlo diventare un tensore di rango 2 (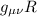 ).
).
Allora il nostro tensore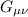 che deve essere lineare nelle derivate seconde e quadratico nelle prime, lo posso scrivere come combinazione lineare, del tensore di ricci e dello scalare di curvatura (che per ipotesi sono lineari nelle derivate seconde e quadratico nelle prime).
che deve essere lineare nelle derivate seconde e quadratico nelle prime, lo posso scrivere come combinazione lineare, del tensore di ricci e dello scalare di curvatura (che per ipotesi sono lineari nelle derivate seconde e quadratico nelle prime).
Allora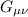 avrà questo aspetto:
avrà questo aspetto:
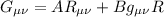
dove A e B sono dei semplici numeri da determinare.
Bisogna ancora applicare la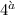 e
e 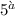 ipotesi.
ipotesi.
Usando la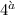 cosa possiamo ricavare?
cosa possiamo ricavare?
Basta calcolare la divergenza covariante di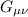 e imporla = 0
e imporla = 0
Facciamolo.
Ora la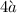 condizione però ha gli indici in alto
condizione però ha gli indici in alto 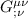 mentre il nostro
mentre il nostro 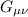 li ha bassi, si può facilmente dimostrare che posso alzare e abbassare gli indici (IN QUESTO CASO) senza problemi, quindi;
li ha bassi, si può facilmente dimostrare che posso alzare e abbassare gli indici (IN QUESTO CASO) senza problemi, quindi;
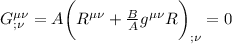
Adesso invece di proseguire in questo calcolo usiamo una famosa identità (identità di bianchi):
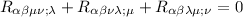
Contraiamo questa espressione con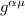 per ogni singolo elemento dentro la parentesi
per ogni singolo elemento dentro la parentesi
cioè:
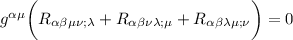
iniziamo dal primo
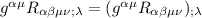 , ho portato
, ho portato 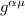 dentro la derivata covariante e lo posso fare perche la derivata covariante di
dentro la derivata covariante e lo posso fare perche la derivata covariante di 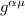 è nulla.
è nulla.
Nell'ultima espressione si contraggono 1° e 3° indice e quindi otteniamo:
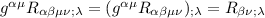
continuiamo con il 3°
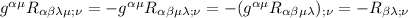
che è lo stesso passaggio di prima, solo che appare quel segno meno, perche nel primo passaggio ho invertito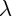 con
con 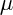 e questo comporta la comparsa del segno meno, visto che il tensore di Riemann è antisimmetrico.
e questo comporta la comparsa del segno meno, visto che il tensore di Riemann è antisimmetrico.
Il 2° pezzo lo lasciamo tale e quale, allora arriviamo alla seguente equazione:
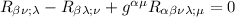
che la contraiamo ulteriormente con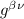
quindi avremo da fare
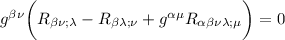
distribuiamo
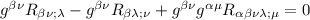
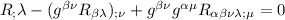
il primo termine si contrae e diventa uno scalare, nel secondo termine ho portato g dentro la derivata covariante come prima, e si contrarrà diventando
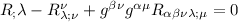
Nell'ultimo pezzo di questa espressione ci lavoriamo un poco sopra, anzitutto commuto le 2 g,
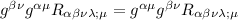
entro nella derivata covariante
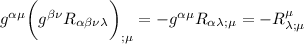
Quindi alla fine l'identità di Bianchi diventa
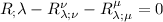
Notare la similitudine dei 2 ultimi termini che sono entrambi derivati in modo covariante per lo stesso indice in altro, allora li sommo (l'indice non è nulla di fisico, in questo caso posso rinominarli) ottenendo;
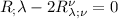
Contraendo con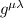 giuro è l'ultima volta
giuro è l'ultima volta 
che succede?
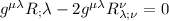
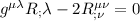
anche qui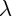 risulta essere indice muto allora lo rinomino in
risulta essere indice muto allora lo rinomino in 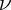
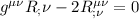
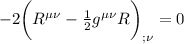
che confrontata con:
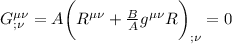
possiamo dire che sono uguali, e abbiamo scoperto che il rapporto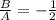
Vedremo come scoprire A nel prossimo post.Ultima modifica di mazzolatore; 17-11-2021 alle 23:12
Dobson Skyliner 200/1200, Celestron OMNI - 6mm 50°, SvBony 105, explore scientific - 32mm 62°, Celestron Up Close G2 10X50
-
-
18-11-2021, 20:02 #2Nana Bruna


- Data Registrazione
- Jul 2016
- Località
- Cisterna di Latina
- Messaggi
- 271
- Taggato in
- 30 Post(s)


Re: Ricavare le equazioni di Einstein
Vediamo come scoprire il valore di A, e successivamente arrivare alle fantomatiche equazioni.
Fortunatamente nel discorso fatto fin'ora non abbiamo ancora utilizzato la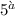 condizione, proprio usando questa possiamo ricavare A.
condizione, proprio usando questa possiamo ricavare A.
Come già menzionato questa condizione ci dice che per campi deboli (non in prossimità di buchi neri per capirci, ma comunque @manzonis ci ha dato un'idea della correzione al campo piatto quanto possa essere), basse velocità e campo stazionario la fisica gravitazionale, si deve tradurre in quella classica di Newton.
Trascriviamo queste 3 condizioni in matematichese.
a -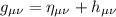 con
con 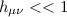 campo debole
campo debole
b -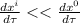 basse velocità
basse velocità
c -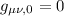 stazionario
stazionario
Tutto ciò come già detto implica che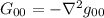
Andiamo a vedere come possiamo scrivere il Tensore di Ricci, sotto queste ipotesi.
In generale l'espressione del tensore di Ricci è la seguente:
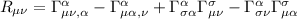
Dove ciascun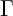 è il simbolo di Christoffel i quali dipendono dalla metrica
è il simbolo di Christoffel i quali dipendono dalla metrica 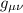 ma dalla condizione a, la metrica puo essere espressa come la metrica piatta più una piccola perturbazione, quindi ciascun simbolo diventerebbe così;
ma dalla condizione a, la metrica puo essere espressa come la metrica piatta più una piccola perturbazione, quindi ciascun simbolo diventerebbe così;
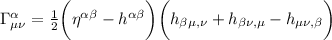
Ora se facessimo tutti i prodotti otterremo dei termini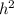 , ma
, ma 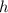 è già una perturbazione molto piccola, se ne facessimo il quadrato sarebbe ancora piu piccola, quindi possiamo tralasciare i termini in
è già una perturbazione molto piccola, se ne facessimo il quadrato sarebbe ancora piu piccola, quindi possiamo tralasciare i termini in 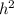
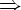
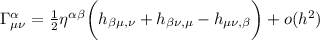
Inoltre come si vede dall'espressione del tensore di Ricci , gli ultimi 2 termini sono il prodotto di due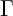 , ciascuna di ordine
, ciascuna di ordine 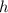 (per l'approssimazione appena fatta), che genererebbero termini di ordine
(per l'approssimazione appena fatta), che genererebbero termini di ordine 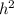 , allora anche quegli 2 ultimi termini sono trascurabili, quindi il tensore di Ricci sarà solamente:
, allora anche quegli 2 ultimi termini sono trascurabili, quindi il tensore di Ricci sarà solamente:
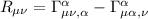
Che scritto esplicitamente è:
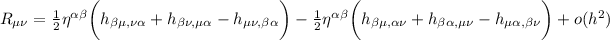
Facendo i calcoli, vediamo che alcuni termini si sommano altri si sottraggono
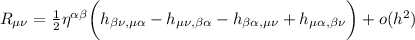
Diventando infine:
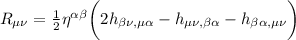
Calcolando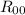 , otterremmo:
, otterremmo:
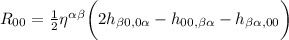
Ma per l'ipotesi c il campo deve essere stazionario, cioè non deve dipendere dal tempo, ergo le derivate di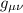 rispetto al tempo (
rispetto al tempo (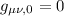 ) sono nulle.
) sono nulle.
Di conseguenza anche le derivate della perturbazione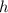 , rispetto al tempo sono nulle, quindi che succede?
, rispetto al tempo sono nulle, quindi che succede?
Che sono 1 di quei 3 termini sopravvive, l'unico che non ha le derivate rispetto al tempo
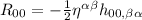
Visto che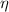 è una matrice 4x4 diagonale (metrica di minkowsky), considerando che non posso utilizzare
è una matrice 4x4 diagonale (metrica di minkowsky), considerando che non posso utilizzare 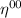 , l'ultima espressione ci diche che:
, l'ultima espressione ci diche che:
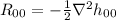 cioè è legato alla divergenza al quadrato di h_{ 0 0 }
cioè è legato alla divergenza al quadrato di h_{ 0 0 }
Questa espressione che l'andremo a sostituire nella formula di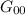
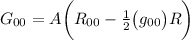
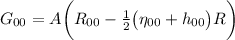
che diventa:
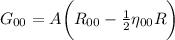
Perche R è di ordine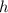
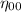 nella metrica di minkowsky vale -1
nella metrica di minkowsky vale -1
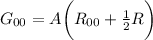
Che andrà confrontata con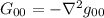
quindi
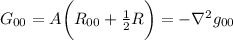
Per stimare A perciò ci basta trovare R.
Usiamo l'ipotesi di basse velocità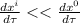 che si traduce in:
che si traduce in:
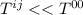
Basta infatti vedere la forma del Tensore energia impulso, per particelle
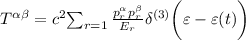
Essendo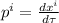 e
e 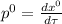 è chiaro che se
è chiaro che se
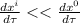
\Rightarrow
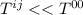
Questo ci è utile proprio adesso perchè per stimare A rimane da calcolare
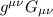
Dove per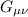 conosciamo 2 espressioni:
conosciamo 2 espressioni:
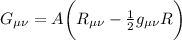
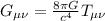
Passiamo a fare il calcolo
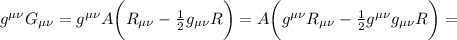
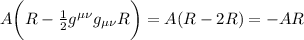
Mentre
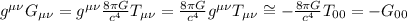
\Rightarrow
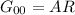
D'altro canto
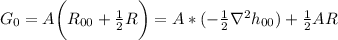
\Rightarrow
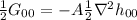
ma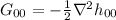
\Rightarrow
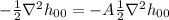
il che significa che A = 1
Quindi l'espressione di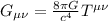
può essere uguagliata a:
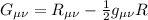
ottenendo
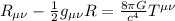
Che sono le equazioni di Einstein, sono al plurale perché gli indici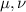 variano da 0 a 3 , quindi 4 indici, e tutte le possibili combinazioni sono 16.
variano da 0 a 3 , quindi 4 indici, e tutte le possibili combinazioni sono 16.
Quindi sono 16 equazioni, che costituiscono un sistema di equazioni differenziali, non lineari, alle derivate parziali.
Un bel casino, ma pur essendo cosi complicato il sistema, in determinate condizioni si semplifica notevolmente e consente delle soluzioni analiticheUltima modifica di mazzolatore; 18-11-2021 alle 22:15
Dobson Skyliner 200/1200, Celestron OMNI - 6mm 50°, SvBony 105, explore scientific - 32mm 62°, Celestron Up Close G2 10X50
-
19-11-2021, 08:24 #3Staff • Moderatore Globale










- Data Registrazione
- May 2012
- Località
- Tarquinia (VT)
- Messaggi
- 29,048
- Taggato in
- 2393 Post(s)




Re: Ricavare le equazioni di Einstein
ti dico mi piace... sulla fiducia!

-
19-11-2021, 08:44 #4Pulsar





- Data Registrazione
- Oct 2013
- Località
- Giugliano in Campania Napoli
- Messaggi
- 8,142
- Taggato in
- 844 Post(s)


Re: Ricavare le equazioni di Einstein
@etruscastro in pochi l’avrebbero fatto 🤣👏👏👏
Lascia che l'anima rimanga fiera e composta di fronte ad un milione di universi
-
19-11-2021, 19:13 #5
-
19-11-2021, 20:57 #6Nana Bruna


- Data Registrazione
- Jul 2016
- Località
- Cisterna di Latina
- Messaggi
- 271
- Taggato in
- 30 Post(s)


Re: Ricavare le equazioni di Einstein
Una soluzione esatta alle equazioni di Einstein è stat ricavata da Schwarzschild niente popò di meno che 2 mesi dopo la pubblicazione dell'articolo di Einstein.
La soluzione proposta da Schwarzschild descrive il campo gravitazionale esterno a qualsiasi oggetto a simmetria sferica NON rotante.
Perciò le ipotesi di Schwarzschild erano 3:
1-Usare le equazioni di Einstein nel vuoto
2-Staticità
3-Simmetria sferica
L'ipotesi di vuoto è immediata da tradurre matematicamente
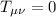
Il tensore energia impulso deve essere nullo, siamo nel vuoto d'altronde.
La richiesta di staticità (del campo gravitazionale) in questo ambito è più sottile, per semplicità immaginiamo la staticità sinonimo di stazionarietà, cioè il campo non cambia nel tempo, il che significa che se facciamo le derivate rispetto la coordinata temporale (che ci dicono la variazione del campo nel tempo) saranno nulle.
Più brevemente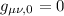
Dove quel 0 sta per derivata rispetto al tempo, 1 sta per coordinata x, 2 = y , 3 = z.
La metrica sotto queste ipotesi è la seguente:
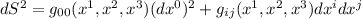
Con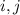 che valgono 1,2,3, cioè rappresentano le 3 variabili spaziali.
che valgono 1,2,3, cioè rappresentano le 3 variabili spaziali.
Da notare che non ci sono i termini misti, cioè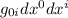
La richiesta di sfericità, che cosa comporta invece?
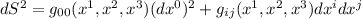
Che l'ultimo pezzo della metrica lo possiamo scrivere con le coordinate sferiche 3D.
E senza troppi sofismi lo possiamo scrivere così:
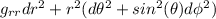
Quindi la metrica è ridotta a questo:
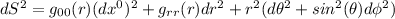
Ora giusto per completezza è da notare che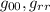 , dipendono esclusivamente dalla coordinata radiale, infatti la dipendenza temporale è stata esclusa dalla stazionarietà, e la dipendenza da
, dipendono esclusivamente dalla coordinata radiale, infatti la dipendenza temporale è stata esclusa dalla stazionarietà, e la dipendenza da 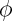 e
e 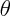 è stata esclusa dalla sfericità.
è stata esclusa dalla sfericità.
Qui viene il punto centrale della situazione, possiamo scrivere
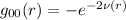
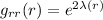
con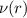 e
e 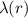 funzioni incognite.
funzioni incognite.
Ma non ricordo il perchè
Non so se hanno qualcosa il particolare oppure è solo una questione di comodità rilegare l'incognita di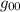 e
e 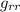 a
a 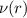 e
e 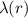
Ad ogni modo scelte queste 2 funzioni (che ripeto devono essere determinate)
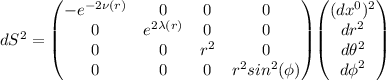
Possiamo ora calcolare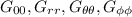
Tramite l'equazione di Einstein trovata nello scorso post.
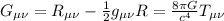
ma: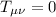
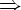
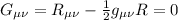
E si fanno i calcoli per ciascun termine , che sono 16, e per ciascuno bisogna calcolare l'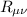 in particolare.
in particolare.
cioè se volessi calcolare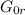 dovrei fare:
dovrei fare:
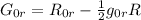
dove
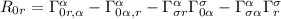
Ecc ecc.
Come detto prima le uniche che sopravvivono sono:
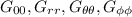 , lo si vede ad occhio notando che la matrice è diagonale, sopravvivono sono i termini diagonali, quindi da 16 a 4, è gia un bel risparmio di forze.
, lo si vede ad occhio notando che la matrice è diagonale, sopravvivono sono i termini diagonali, quindi da 16 a 4, è gia un bel risparmio di forze.
I risultati sono:
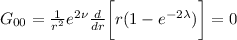
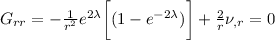
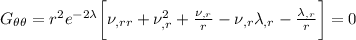
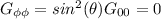
Vi risparmio la risoluzione di questo sistema e vi lascio la soluzione:
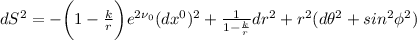
Facendo una leggera trasformazione, estetica diventa:
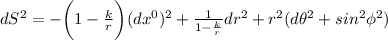
dove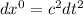 e
e 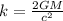
quindi:
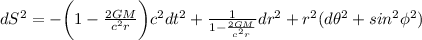
Questa viene detta Soluzione di Schwarzschild, notare che è una soluzione ESATTA, dove non abbiamo fatto alcuna approssimazione.
Che descrive lo spazio-tempo attorno a una massa sferica, non rotante e priva di carica elettrica.Dobson Skyliner 200/1200, Celestron OMNI - 6mm 50°, SvBony 105, explore scientific - 32mm 62°, Celestron Up Close G2 10X50
-
19-11-2021, 21:03 #7Nana Bruna


- Data Registrazione
- Jul 2016
- Località
- Cisterna di Latina
- Messaggi
- 271
- Taggato in
- 30 Post(s)


Re: Ricavare le equazioni di Einstein
Il parametro
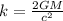 viene detto Raggio di Schwarzschild.
viene detto Raggio di Schwarzschild.
Tale parametro è quello che mi crea delle singolarità nella metrica di Schwarzschild. Che non vanno confuse con la singolarità del buco nero.
Un buco nero è un corpo che ha un Raggio < del Raggio di Schwarzschild.
Per il sole vale 2.9km
Per la terra 8.9 millimetri.
Per la via lattea 0.2 anni luce.
Dobson Skyliner 200/1200, Celestron OMNI - 6mm 50°, SvBony 105, explore scientific - 32mm 62°, Celestron Up Close G2 10X50
0.2 anni luce.
Dobson Skyliner 200/1200, Celestron OMNI - 6mm 50°, SvBony 105, explore scientific - 32mm 62°, Celestron Up Close G2 10X50
-
19-11-2021, 21:24 #8
Re: Ricavare le equazioni di Einstein
Anche io ti seguo a fiducia. Bravissimo.
"Non so nulla con certezza, ma la vista delle stelle mi fa sognare"
Classic 8" Cassegrain, NW 150/750, EQ5 synscan, SV305pro, Asi 585, Q-Barlow Baader
-
20-11-2021, 13:22 #9
Re: Ricavare le equazioni di Einstein
Beh, che dire... anch’io a fiducia, e neanche seguo
 complimenti e grazie per l’iniziativa.
complimenti e grazie per l’iniziativa.
Mi sorge una curiosità da profano: con la relativita’ generale Einstein riuscì a giustificare una discrepanza di 43 arcosecondi/secolo nell’orbita di Mercurio rispetto a quella calcolata teoricamente in base alle fisica classica di Newton. In precedenza alla scoperta di Einstein era stata ipotizzata l’esistenza di un ulteriore pianeta (Vulcano) vicino al Sole la cui attrazione gravitazionale su Mercurio avrebbe spiegato tale discrepanza (un po’come le “perturbazioni” nell’orbita di Urano, che hanno consentito di arrivare alla scoperta di Nettuno per via teorica, prima della sua effettiva osservazione).
Queste formule c’entrano qualcosa o si riferiscono a tutt’altro?To see a World in a Grain of Sand And a Heaven in a Wild Flower...
-
20-11-2021, 13:30 #10
Re: Ricavare le equazioni di Einstein
grazie mazzolatore
Un altro post impeccabile , non solo per fiducia dato che qualcosa , questa volta l'ho capita
solo per curiosità
le equazioni differenziali di Einstein come molte altre della fisica sono non lineari , la soluzione analitica è quasi sempre impossibile
Per casi più complessi di quello citato si ricorre quindi al calcolo numerico
Che tu sappia in ambito accademico o professionale si usano software tipo Mathematica o Matlab oppure si implementano algoritmi dedicati ad ogni particolare equazione in C or Python o altri linguaggi di programmazione ?
chiedo questo in quanto mi diletto a risolvere e equazioni differenziali alle derivate parziali con il metodo delle differenze finite in python
per equazioni non omogenee e non lineari la complessità dell'algoritmo di calcolo cresce esponenzialmente
Ho anche Mathematica e Matlab ma con certe equazioni non funzionano e non c'è verso di farli funzionareUltima modifica di Albertus; 20-11-2021 alle 13:39
-
Discussioni Simili
-
Einstein Telescope
Di corrado973 nel forum AstrofisicaRisposte: 4Ultimo Messaggio: 25-02-2018, 12:51 -
Anello di Einstein
Di corrado973 nel forum AstrofisicaRisposte: 6Ultimo Messaggio: 14-08-2016, 15:20 -
Einstein resiste ancora
Di Enrico Corsaro nel forum NewsRisposte: 2Ultimo Messaggio: 13-05-2016, 21:07 -
Einstein e Eddington...
Di aenimanimal nel forum AstrofisicaRisposte: 4Ultimo Messaggio: 19-09-2014, 19:58 -
Energia e materia oscura? Nessun problema: basta cambiare un poco le equazioni di Einstein
Di Vincenzo Zappalà nel forum ArticoliRisposte: 4Ultimo Messaggio: 14-09-2012, 08:56




 Rispondi Citando
Rispondi Citando
















Nebulosa IC1396 [APOD 20-07-2025]
Oggi, 08:45 in APOD by Astronomia.com