Discussione: dubbio meccanica orbitale
-
20-08-2015, 11:09 #1
dubbio meccanica orbitale
Buongiorno ragazzi,
ho un dubbio sulla meccanica orbitale e non riesco a venirne fuori. Premetto che conosco la fisica (laurea in ingegneria) ma sono quei dubbi che ti assalgono e non riesci a venirne fuori. In pratica parlando di orbite, sappiamo che ad un orbita più lontana è associata una minore velocità orbitale mentre ad una più stretta una maggior velocità orbitale. Se però io ho un oggetto (pianeta o satellite che sia) e voglio allargarne l'orbita devo aumentarne la velocità, concetto però in contrasto con quanto detto prima, cioè ad un orbita più larga corrisponde una minor velocità orbitale. Ad esempio se la terra rallentasse "cadrebbe" verso il sole o restringerebbe la sua orbita, ma secondo quanto constatato prima una minor velocità dovrebbe corrispondere un'orbita più allargata e non più stretta.
Quindi se io ho 2 satelliti alla stessa altezza (quindi stessa orbita) avranno ovviamente la stessa velocità orbitale, ma se ne accelero uno aumentandone la velocità questo si sposta su un orbita più "alta" quindi più ampia, ma secondo quanto detto prima non dovrebbe avere una minor velocità rispetto al satellite più "basso"?
A me sembra un paradosso, ma la spiegazione credo che risieda nella conservazione del momento angolare ma riesco a capire come. qualcuno può darmi una spiegazione esauriente?
Grazie!
-
-
20-08-2015, 18:44 #2
Re: dubbio meccanica orbitale
Ciao @luca.g !
Leggendo il tuo messaggio noto che come si dice alle volte ti sei "incartato" da solo .
.
Ti rispondo a seguire in modo da chiarirti il dubbio .
.
Qui sussiste il problema di fondo. Da dove hai dedotto che allargando l'orbita di un corpo in moto di rivoluzione la sua velocità debba aumentare? Non esiste alcuna legge che ti dice che questo debba accadere, anzi al contrario, poichè il momento angolare deve conservarsi, se aumenti la dimensione dell'orbita deve di conseguenza diminuire la velocità orbitale del corpo.
Se la Terra rallentasse la sua velocità, non cadrebbe verso il Sole ma al contrario la sua orbita si allargherebbe, allontanandola così dalla Terra. Questo sempre per la conservazione del momento angolare, che per mantenersi costante deve compensare la diminuzione di velocità orbitale con un aumento della distanza dal Sole. La conservazione del momento angolare è una delle leggi fondamentali della dinamica di sistemi dove agisce l'effetto di rotazione.
No, per quanto detto prima, se aumenti la velocità di un satellite quello che causi è di avvicinarlo invece di allontanarlo dal centro di rotazione. Infatti il paradosso che hai sollevato non sussiste affatto. Mi rendo conto che a primo acchito non è un discorso molto intuitivo ma per capirlo bene devi appunto tenere a mente il momento angolare del sistema.
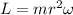
dove m è la massa del corpo, r la sua distanza dal centro di rotazione e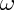 la velocità angolare. Perchè L sia costante, se aumenti r, deve diminuire
la velocità angolare. Perchè L sia costante, se aumenti r, deve diminuire 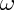 , e viceversa.
, e viceversa.
-
20-08-2015, 19:39 #3
Re: dubbio meccanica orbitale
Ciao Grazie per la risposta!ma è esattamente ciò che dico io!
Mettiamola così: se io ho un satellite che orbita attorno alla terra, e incontra la resistenza dell'aria RALLENTANDO, questo "cade" sempre più verso la terra poichè la forza centrifuga data dalla velocità non riesce più a equilibrare l'attrazione gravitazionale. Ed è palese dalle formule del moto che se voglio allargare l'orbita di un satellite e "allontanarlo" dalla terra devo accelerarlo, fornendo energia cinetica che poi si convertirà in energia potenziale su un orbita più "alta". Ergo lo stesso dovrebbe succedere alla terra: ad esempio se dovesse venir rallentata in qualche modo non avrebbe più la velocità sufficiente per orbitare e sarebbe attratta dal sole, esattamente come un satellite cadrebbe verso la terra. Ciò però è in contrasto proprio con quello che hai detto tu e io: e cioè il fatto che ad un orbita più esterna corrisponde una MINOR velocità orbitale, infatti i pianeti più esterni hanno una velocità orbitale via via minore. Da qui nasce il mio dubbio: cosa succede se io rallento o accelero un corpo in orbita??Se la terra venisse "accelerata" tipo con degli enormi razzi (ipotesi fantascientifica) questa allargherebbe la sua orbita, perchè tenderebbe a"sfuggire" all'attrazione gravitazionale del sole..ovviamente come avevo previsto l'inghippo sta nella conservazione del momento angolare, che però non riesco ad applicare.Ultima modifica di etruscastro; 21-08-2015 alle 09:30 Motivo: non quotare per intero il messaggio immediatamente precedente!
-
20-08-2015, 20:06 #4
Re: dubbio meccanica orbitale
Una cosa è valutare un cambiamento in orbita senza ulteriori considerazioni, un'altra è considerare che interviene una forza esterna al tuo sistema. Per sistema in questo caso ci dobbiamo riferire all'intero Sistema Solare.
Se ci sono in gioco forze esterne che cambiano il tuo sistema allora il momento angolare non è più soggetto a conservazione. Bisogna dunque capire in che termini valuti il cambiamento. Se agisce qualcosa dall'esterno, ad esempio per dirne una l'impatto con un grosso corpo o un altro evento cataclismico che è generato da qualcosa proveniente dall'esterno del Sistema Solare (ad un corpo vagante che va a collidere con la Terra o l'esplosione di una stella vicina che genera forti onde di pressione e spostamenti di mezzo interstellare), allora la conservazione del momento angolare si rompe.
L'esempio del rallentamento a causa di resistenza con il mezzo interplanetario (e non con l'aria) non è di fatto un esempio di forza esterna. Questo perchè il momento angolare di cui gode la Terra è legato a quello dell'intero Sistema Solare, per motivi di formazione collettiva. Per rompere la conservazione del momento angolare terrestre, ti occorrerebbe allora un evento cataclismico dall'esterno come ti ho già detto prima.
No non è in contrasto, se reputi che il cambiamento sia avvenuto per effetto di forze esterne al sistema. Se una forza agisce da fuori, come ti citavo prima, allora tutto può cambiare.
Invece nell'esempio che hai fatto, non potrai cambiare il momento angolare totale perchè stai agendo dall'interno. Ci sono due possibili casi da considerare ipotizzando di usare dei grandi razzi come tu dici:
1) Se acceleri lungo la direzione dell'orbita puoi cambiare la velocità orbitale della Terra accelerandola ma, non sei in grado di cambiare il momento angolare totale del Sistema Solare, perchè stai agendo dal suo interno. Anche se dunque la velocità orbitale della terra accelera, il momento angolare totale del Sistema Solare non può cambiare e di conseguenza deve diminuire la dimensione dell'orbita della Terra.
2) Se invece agisci con una forza in direzione ortogonale al moto orbitale, causerai un cambiamento nel raggio dell'orbita (assumendo sia circolare per semplicità) e di conseguenza il momento angolare per mantenersi costante farà si che la velocità orbitale della Terra diminuisca.
Spero di essere stato chiaro .
.
-
20-08-2015, 20:23 #5
Re: dubbio meccanica orbitale
Si certo, ti seguo perfettamente, ma come dici per avere una "caduta" della terra verso il sole cosa dovrebbe accadere?solo un evento esterno al sistema solare?se intervengo con dei fantascientifici razzi?Inoltre il mio discorso non è legato solamente alla terra, ma ai moti orbitali in generale. Che mi dici dei satelliti? Se io accelero un satellite in orbita in direzione tangenziale al moto la sua orbita si allarga giusto? E cosa succede alla sua velocità?io l'ho aumentata con una spinta, ma una volta posizionatosi sulla nuova orbita la velocità resta la stessa che io ho impresso? o rallenta portandosi al valore di velocità richiesto per quella nuova orbita? Spero di aver chiarito quali sono i miei dubbi..in sintesi:
secondo le formule di equilibrio di forza centrifuga e forza gravitazionale e dal momento angolare risulta ovviamente che V ed r sono inversamente proporzionali; aumenta V diminuisce r e viceversa, e fin qui ci sono.
Supponiamo con dei numeri che per stare in una certa orbita 1 la mia velocità debba essere di 9 km/s (numeri puramente indicativi eh). Nel momento in cui io rallento a 2 km/s a causa di una forza esterna (che siano la resistenza dell'aria, dei razzi che frenano, l'impatto con qualcosa) sono portato a pensare che la mia velocità (e quindi la forza centrifuga) non è più sufficiente a restare in quell'orbita e vincere l'attrazione, di conseguenza prevalendo ora l'attrazione gravitazionale l'oggetto cade verso il centro di attrazione...ergo la sua orbita si stringe..ovviamente il mio dubbio è che ciò contrasta con le formule, che dicono che a minor velocità (passo da 9 a 2 km/s) dovrebbe corrispondere un'orbita più ampia..da qui nasce il mio paradosso..a questo punto vogliamo ragionare con le formule avanti?
Infine se parlassi di manovra orbitale per posizionare ad esempio una navetta da un'orbita 1 ad un'orbita 2 + "alta" (quindi più larga) cosa dovrei fare?Credo accendere i razzi ed aumentarne la velocità tangenziale in modo da allargarne l'orbita, dopodichè accendere dei retrorazzi e rallentarla fino alla velocità richiesta dalla fisica per restare in quell'orbita giusto? (essendo l'orbita più larga la navettà dovrà avere una velocità minore rispetto a quella che aveva sulla prima orbita)Ultima modifica di etruscastro; 21-08-2015 alle 09:31 Motivo: no quoting!!
-
20-08-2015, 22:07 #6
Re: dubbio meccanica orbitale
Allora procediamo con ordine. Per prima cosa ti chiedo di evitare di quotare l'intero messaggio, altrimenti diventa difficile leggere il tutto (è anche una regola del forum).
Se parliamo di un pianeta, l'inerzia (data dalla massa in gioco) è talmente grande che nessun tipo di razzo ti permetterebbe comunque di cambiare il momento angolare totale, quello del pianeta e dunque del Sistema Solare. Per modificare il momento angolare di un pianeta, dovresti agire contemporaneamente su due fronti: da un lato ad esempio rallentare la sua velocità orbitale e dall'altro, impedire che la sua orbita si allarghi (moto radiale) a causa della conservazione del momento angolare. Se riesci a vincere questi due moti allora avrai modificato il momento angolare del pianeta. Puoi però cambiare l'orbita di un pianeta, senza contrastare la conservazione del momento angolare, agendo quindi sulla sua velocità orbitale. Contrastare la conservazione del momento angolare è molto difficile perchè richiede energie paragonabili a quelle in gioco per effetto dello stesso campo gravitazionale. Più è grande la massa in gioco, più difficile diventa variarne il momento angolare.
Se parliamo di satelliti artificiali e asteroidi il discorso cambia, perchè la loro massa è enormemente più piccola. Puoi dunque imporre tu un momento angolare agli stessi, operando come ti ho appena scritto prima.
Infatti, se ti limiti a variare la velocità orbitale di un satellite, per la conservazione del momento angolare esso si disporrà su di una orbita differente. Per mantenere la stessa orbita e al contempo aumentare (o diminuire) la sua velocità, è necessario che tu intervenga in due direzioni fondamentali, quella tangenziale e quella perpendicolare al moto di rivoluzione.
Il principio di base da considerare è che il moto orbitale è causato unicamente dalla concomitanza di due fattori: 1) la forza gravitazionale e 2) la conservazione del momento angolare. Se uno dei due decade, non hai più moto orbitale.
Per valutare il caso che discuti dobbiamo parlare in termini di entità della variazione.
Se tu rallenti gradualmente la tua velocità per effetto di un agente esterno che si oppone al tuo moto allora gradualmente cambierai anche la tua orbita per effetto del momento angolare e non necessariamente cadrai al centro perchè il momento angolare tende a conservarsi. Anche se infatti lo cambi leggermente, se la variazione è leggera il sistema ritenderà all'equilibrio così rapidamente da impedire alla forza di gravità di prendere il sopravvento, operando quindi sulla tua orbita e allontanandoti dal centro. Se però il cambiamento alla velocità orbitale è veramente forte e drastico, può accadere che come dici, nel tuo stesso sistema di riferimento la tua velocità orbitale si trova improvvisamente ad essere così bassa da fornirti una forza centrifuga che non è sufficiente a contrastare la forza gravitazionale, e pertanto cadrai verso il centro. Questo è tanto più facile che si realizzi tanto più piccola è la massa del corpo in orbita e tanto più grande è l'attrazione gravitazionale in gioco.
Il problema di base è conferire al satellite quel momento angolare iniziale. Una volta fatto, è meno complicato cambiare la sua orbita perchè basta variare la sua velocità orbitale, appunto nel tuo caso rallentandola in modo da farlo migrare ancora più esternamente, per quanto ti ho già detto prima. Quindi il succo del discorso è che devi pensare a portare il satellite nell'orbita più conveniente per i tuoi scopi, investendo dunque le tue energie nella fase iniziale che lo porta dall'essere fermo al ritrovarsi in orbita con una determinata velocità.
Chiaramente più è drastico il cambiamento di orbita che vuoi realizzare, più energia ti servirà per variare il moto dello stesso satellite.
Quindi riassumendo:
Se tu modifichi la velocità orbitale oppure ti sposti radialmente verso una orbita più piccola o più grande, non puoi cambiare il momento angolare, che dunque ricompenserà subito la variazione che hai introdotto cambiando il parametro complementare. Se invece operi in contemporanea su entrambi, allora potrai cambiare il momento angolare. Tuttavia, tanto più è la massa che vuoi spostare, tanta più energia ti servirà e nel caso dei pianeti diventa impensabile da parte nostra poter riuscire in questa impresa.
-
20-08-2015, 22:29 #7
Re: dubbio meccanica orbitale
Bella discussione. Grazie a entrambi
mi chiedo @Enrico Corsaro quando vi erano le missioni Apollo il razzo vettore doveva raggiungere la velocita di 26.000 km all'ora ossia circa 7,2 km al sec.
Il modulo per lanciare Apollo verso la Luna doveva portare la velocità di fuga a 11 km al sec.
Quindi...so che esiste la conservazione del moto angolare che è quello che a fatto fare i suoi giri a Giove ma qui qual'è il punto di vista in questa situazione? Portando la velocita a 11 km al secondo apollo non scendeva in un'orbita stretta ma andava sulla luna
-
20-08-2015, 23:24 #8
Re: dubbio meccanica orbitale
esattamente quel che dicevo io. per allargare l'orbita occorre accelerare il mezzo. poi credo sia stato decelerato perché essendo l'orbita più larga l'oggetto necessita di una minor velocità per stare in orbita. per quanto riguarda la massa della terra rispetto a quella dei satelliti è ovvio che per accelerare la terra servirebbe una energia enorme, infatti il mio era solo un discorso a livello di ipotesi. come vale per i satelliti vale anche per la terra anche se le masse in gioco sono diverse (e ovviamente anche le energie), ma concettualmente è la stessa cosa. Ovvio che non esistono razzi che accelerano la terra (non crederai che fossi convinto di questo spero?). il mio era solo un discorso per fare l'esempio..
-
20-08-2015, 23:31 #9
Re: dubbio meccanica orbitale
@luca.g certamente, direi che ci siamo capiti e anche il mio discorso vale in generale. Ma bisogna sempre distinguere in base alla massa in esame e al tipo di sistema. Un pianeta nel nostro sistema è in un contesto particolare perchè è parte del Sistema Solare. Un satellite mandato in orbita è invece qualcosa che viene prima costruito sulla Terra e a cui viene poi imposto un momento angolare tramite l'uso di una forza che possiamo controllare.
Tieni quindi sempre a mente il tipo di effetto e la direzione del moto che vogliamo imporre.
Se parliamo delle missioni Apollo, non c'è unicamente il discorso orbitale, ma anche quello direzionale specifico per mandare le missioni verso la Luna. Bisogna prima di tutto vincere la forza gravitazionale in quel caso, quindi accelerando il razzo, altrimenti non possiamo mandare un satellite in orbita, dal momento che di base parte da fermo. Una volta in orbita poi è il momento angolare a governare la dinamica.
-
20-08-2015, 23:37 #10
Re: dubbio meccanica orbitale
ma se ho ben capito vuoi dire che la modifica di un solo moto orbitale di un pianeta va a modificare quello di tutti gli altri?mi spiego meglio. tu consideri il momento angolare di tutto il sistema solare?io pensavo che ogni sistema di 2 corpi avesse il suo momento angolare, come ad esempio momento angolare sistema mercurio-sole, terra-sole, marte -sole ecc..quindi nella mia concezione la modifica del momento angolare del sistema mercurio-sole non influisce sul momento del sistema giove-sole o terra-sole ecc..quindi se ad esempio la terra rallenta o si avvicina al sole o si allontana gli altri pianeti continuano a orbitare come stavano facendo..
-
Discussioni Simili
-
Moto orbitale ?
Di etto64 nel forum Meccanica CelesteRisposte: 6Ultimo Messaggio: 01-04-2015, 13:02 -
6. Meccanica quantistica: come tutto è cominciato.... Parte I
Di Red Hanuman nel forum ArticoliRisposte: 9Ultimo Messaggio: 07-10-2013, 22:48 -
1. Come affrontare la Meccanica Quantistica.
Di Vincenzo Zappalà nel forum ArticoliRisposte: 38Ultimo Messaggio: 28-08-2013, 06:10 -
Urge una Polizia orbitale
Di Vincenzo Zappalà nel forum ArticoliRisposte: 19Ultimo Messaggio: 08-06-2013, 01:51




 Rispondi Citando
Rispondi Citando













Ciao a tutti
Oggi, 19:55 in Mi presento