Loading ...
1536 visite
I quasar sono oggetti talmente luminosi che superano di molto la luce proveniente dalle centinaia di milioni di stelle che compongono la galassia che li ospita. Questo fatto rende molto difficile studiare le caratteristiche della galassia dominata com’è dal buco nero super massiccio che risiede nel suo “cuore”. Oggi si è potuto finalmente ottenere un notevole risultato invertendo i ruoli degli attori di un classico “effetto lente”.
Immaginate di essere accecati dai fari anteriori di un’automobile e di cercare nello stesso tempo di identificare i colori dei bordi degli stessi fari. Sarebbe un’impresa praticamente impossibile. Ciò è quello che capita quando si cerca di studiare un quasar. Sappiamo benissimo che esso risiede al centro di una galassia ospite, ma la sua straordinaria luce rende impraticabile qualsiasi studio di quest’ultima. D’altra parte sappiamo anche che i quasar sono oggetti solitamente molto lontani (e quindi antichi) che rappresentano fasi primitive della formazione galattica. Sarebbe perciò molto interessante eseguire studi più accurati.
Ancora una volta Einstein ci ha dato una mano. La sua teoria della relatività ci dice che se una grande massa (come una galassia o un gruppo di galassie) si frappone tra noi e un oggetto molto più lontano, la luce di quest’ultimo viene deviata e va a formare una o più immagini ingrandite del corpo celeste altrimenti invisibile. E’ il ben noto effetto chiamato “lente gravitazionale” che gli astronomi conoscono ormai molto bene e che utilizzano solitamente per studiare oggetti primordiali del nostro Universo.
La prima lente gravitazionale fu scoperta nel 1979 ed era relativa ad un quasar disperso e ingigantito da una galassia più vicina. Oggi conosciamo centinaia di questi casi e tramite loro si sono studiati i quasar più lontani. Tuttavia, come già detto, studiare un quasar in questo modo vuole dire avere informazioni sul mostruoso buco nero che domina l’oggetto e non certo sulla galassia che lo ospita e che viene praticamente cancellata dalla luce troppo intensa.
Era necessario poter invertire i ruoli. Ossia, cercare di trovare un quasar più vicino che nascondesse una galassia più lontana e che fosse lui a causare l’effetto lente. Qualcuno chiederà: “Perché”. Presto detto. Lo spostamento della luce causata dal quasar ci darà indicazioni chiare non solo sulla massa del quasar vero e proprio (ossia il buco nero centrale), ma sulla massa totale della galassia che lo ospita. Anche senza vederla, gli effetti causati sulla normale galassia più lontana permettono di leggere ciò che non si vede.
La ricerca è stata lunga, ma alla fine ci si è riusciti. Il quasar SDSS J0013+1523, posto a circa 1,6 miliardi di anni da noi, nasconde dietro di esso una galassia localizzata a 7,5 miliardi di anni. Il telescopio Keck delle Hawaii con i suoi 10 metri di diametro ha eseguito le osservazioni. Ora si potranno finalmente studiare i rapporti di massa tra quasar e galassia ospitante e leggere meglio la loro evoluzione comune, fondamentale per conoscere le prime fasi di formazione galattica.
Sicuramente è stato il primo caso, ma certamente non sarà l’ultimo: lo scambio di ruolo ha risvolti veramente interessanti!
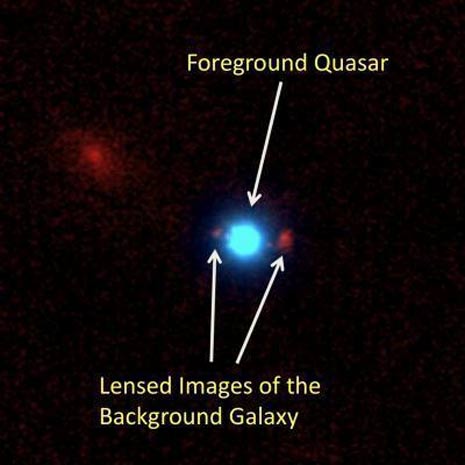
Un’immagine del Keck che riprende il quasar (in blu) che causa la dispersione e l’ingrandimento della galassia molto più lontana (in rosso). L’importanza dell’osservazione sta nello spostamento della luce di quest’ultima causata dalla massa del quasar che causa l’effetto lente gravitazionale. (Fonte: Courbin, Meylan, Djorgovski, et al., EPFL/Caltech/WMKO.)
articolo successivo: Anche grande è bello!
articolo precedente: Una coda di neonati
8 Commenti a “Scambio di ruoli”
@Sandro,
direi proprio di si… anche se la sua luminosità viene ingigantita, il redshift rimane lo stesso.
@Enzo,
ho letto da qualche parte che ci sono quasar distanti quasi 14 miliardi di anni luce da noi, è possibile?
@Silvia,
siamo vicini a scorgere gli oggetti più antichi “visibili”. Il che vuol dire quelli apparsi dopo la cosiddetta “età buia” o dark age. Non è improbabile perciò che alcuni oggetti già osservati, essenzialmente quasar a causa della loro enorme luminosità e antichità, si avvicinino a quel limite, stimato intorno al miliardo di anni dopo il Big Bang. In altre parole dai 13 ai 13.5 miliardi di anni luce da noi, magari anche qualcosa in più. Tieni però conto degli errori nella determinazione delle distanze che si misurano prendendo per esatta la legge di Hubble sul redshift… Diciamo che 14 miliardi è un po’ troppo e che 13.6-13.7 potrebbe anche essere…
Di più è impossibile stimare… 
Ma come si fa ad essere sicuri che le due immagini rosse rappresentino l’immgine sdoppiata della stessa galassia e non invece due galassie distinte in due posizioni differenti?
Vaaaaaaaaaaaaaa bene..mi fido allora! 
Grazie prof!
Una domanza Enzo: il metodo per calcolare la distanza della galassia retrostante il quasar è sempre relativo al redshift della luce deviata? Ci sono altri accorgimenti che vengono tenuti in considerazione?
Grazie