Le magie della rifrazione luminosa

Chi ha letto l’Infinito Teatro del Cosmo sa benissimo che la luce può essere descritta in due modi, entrambi esatti: o come un’informazione trasportata da particelle piccolissime (i fotoni) oppure come un insieme di onde che si propagano nello spazio e che partono dalla sorgente, al pari di ciò che capita quando tiriamo un sasso nell’acqua. Bene, per parlare di telescopi, è molto meglio usare il secondo metodo. Anzi, si può addirittura fare una semplificazione ulteriore, come vedremo tra poco. La Fig. 1 ci mostra una sorgente che invia le sue onde di luce circolari (in realtà sarebbero sferiche nelle tre dimensioni). Se niente le disturba, si allargano sempre più andando a spasso per l’Universo. Una parte di esse può raggiungere l’osservatore che, allora, è in grado di “vedere” la stella. In realtà, per vedere la sorgente, si deve  già usare un primo strumento ottico: l’occhio, con tanto di obiettivo, fuoco e lastra “fotografica” o CCD. Ma andiamo con calma…

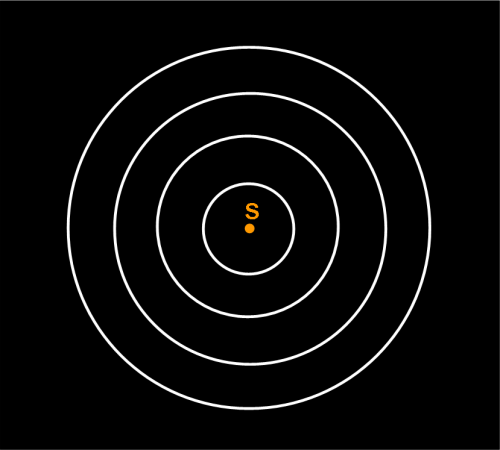
Immaginiamo la nostra stella talmente lontana che le sue dimensioni possano essere considerate trascurabili rispetto alla distanza dell’osservatore. In altre parole, possiamo considerarla una sorgente puntiforme. E quando dico puntiforme dico proprio puntiforme, ossia un vero punto. Talmente piccolo che se riuscissi a vederlo senza alcun difetto dovuto all’occhio, al telescopio, al binocolo o cose del genere dovrei riuscire a vederlo veramente privo di dimensioni (un po’ come il Big Bang…). Tutte le stelle, a parte il Sole, possono essere considerate così. Lasciamo per adesso da parte il punto e vediamo di seguire il suo sistema di onde luminose. Teniamo, però, ben presente questa considerazione che tornerà molto utile più avanti.

Consideriamo la Fig. 2 (che è uguale alla Fig. 1) ed eseguiamo la semplificazione che vi dicevo prima. Invece di disegnare tutte quelle circonferenze, posso benissimo tracciare solo la direzione che parte dal centro e va verso l’esterno, un po’ come facevamo con il palloncino che rappresentava lo spazio e il tempo che partiva dal Big Bang e che definiva istante per istante il raggio del palloncino. In altre parole, invece di disegnare le circonferenze posso disegnare solo le rette che partono dalla stella e che, per definizione, sono sempre perpendicolari alla circonferenza, o, meglio, alla tangente alla circonferenza nel punto in cui la toccano. Esse rappresentano perfettamente le circonferenze: disegnate loro, si possono disegnare subito le circonferenze corrispondenti. 

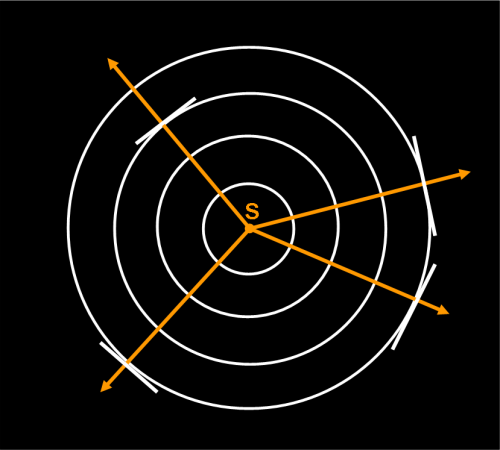
Questi raggi vengono proprio chiamati raggi luminosi e sono più che sufficienti a caratterizzare le onde sferiche.  Lasciamo, per il momento, da parte queste ultime e lavoriamo solo con i raggi. Quando ne avremo bisogno sapremo subito come disegnare anche loro. Per essere “tecnici”, questo tipo di studio della luce prende il nome di ottica geometrica ed è più che sufficiente per definire i vari tipi di telescopio e non solo.

Se il raggio dei cerchi che rappresentano le onde si allunga sempre di più, ossia se la distanza dalla sorgente diventa veramente molto grande, la piccola parte di onda che raggiunge la terra T può essere considerata piana e non circolare. Invece di onde concentriche potremmo tranquillamente considerare onde rettilinee, tutte parallele fra loro, proprio come in una spiaggia davanti al mare aperto, come rappresentato in Fig. 3. a destra. Da che raggi luminosi sarebbero rappresentate queste onde? Facile a dirsi: da un insieme di rette perpendicolari alle linee delle onde, tutte parallele fra di loro. In questo modo abbiamo fatto nostro un primo importantissimo concetto fisico: il fascio luminoso proveniente da una stella può essere disegnato come un insieme di raggi luminosi paralleli tra di loro. Un concetto non così difficile, direi…

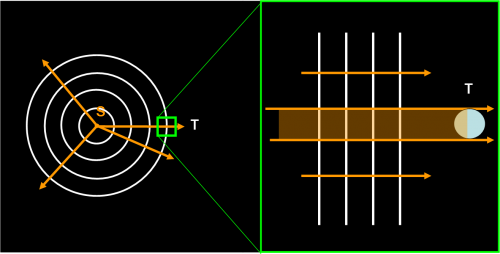
Un fascio praticamente infinito, dato che si estende ovunque nello spazio. Le sue dimensioni sono solo limitate dalla parte che colpisce la Terra (parte arancione nella figura), o l’osservatore o, meglio ancora, il suo prezioso telescopio personale, ossia l’occhio.

Per semplificare ancora le cose, consideriamo un solo raggio che arrivi fino al suolo terrestre (i suoi amici sono uguali e paralleli). Immaginiamo che sia stato così fortunato da non incontrare molecole di gas o di polvere sospese nell’atmosfera. Esso tocca terra (anzi acqua) in un punto, formando un certo angolo con la perpendicolare alla superficie di  un fiume o di un laghetto limpido e trasparente.

Cosa fa il nostro raggio dopo tanto cammino? E’ capace di proseguire anche nell’acqua oppure no? Sicuramente sì, anche se deve subire una modificazione piuttosto importante. In Fig. 4. immaginiamo che la retta z sia la perpendicolare alla superficie d’acqua. Il raggio luminoso, che è arrivato viaggiando nell’aria, forma un certo angolo d’incidenza i con la linea z. Esso penetra nell’acqua, ma viene deviato rispetto alla direzione precedente. In che modo? Semplice, si piega in modo da formare un angolo r (detto di rifrazione) più piccolo, con la retta z, all’interno del liquido.

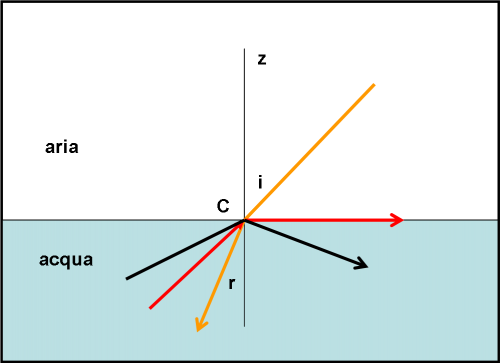
Perché è capitato tutto ciò? Perché l’acqua si oppone in modo diverso al cammino (ottico) del raggio. In realtà, ciò che capita è che il contatto con l’acqua modifica il sistema di onde che provengono dalla stella o da ciò che preferite. Lo modifica cambiando apparentemente la direzione di provenienza. Non sarebbe difficile spiegarlo, ma per adesso accettatelo come un dato di fatto, ci torneremo sopra un’altra volta. Al limite, per farvene un’idea preliminare, pensate a come cambiano le onde quando arrivano sul litorale. L’importante è che il raggio luminoso si avvicini alla perpendicolare tracciata alla linea di separazione tra acqua e aria.

Ogni tipo di sostanza ha un particolare valore che indica quanto il raggio di luce viene deviato al suo interno. Questo parametro si chiama indice di rifrazione: più esso è grande e più il raggio luminoso si avvicina alla perpendicolare z tracciata rispetto al confine tra le due sostanze. In altre parole,  se l’indice di rifrazione di una sostanza cresce, diminuisce l’angolo che il raggio luminoso sottende rispetto alla perpendicolare alla superficie di contatto tra le due sostanze. In formula matematica (aiuto!): r < i. La stessa cosa capiterebbe, ad esempio, se si passasse dall’aria al vetro. Quest’ultimo è proprio il caso che interessa le lenti e quindi i telescopi a lente.

Posso dirvi che abbiamo raggiunto il punto più difficile dell’intera trattazione! Faticoso eh?!

Ovviamente, vale anche il viceversa: se un raggio passo da una sostanza con indice di rifrazione più alto a una con indice più basso, l’angolo aumenta. r diventa angolo di incidenza e i angolo di rifrazione. Esiste, però, un angolo limite o critico. Se l’angolo r raggiunge un certo valore (per l’acqua è 49° e per il vetro 42°) il raggio rifratto, passando dalla prima sostanza all’aria, diventa esattamente di 90°. Ossia il raggio si propaga proprio lungo la superficie (linea rossa). Se poi si supera quest’angolo il raggio torna indietro, ossia viene riflesso completamente (linea nera). Proprio su questo principio si basano le fibre ottiche. Tuttavia, di specchi e di riflessione parleremo in seguito.

Adesso vogliamo capire perché i pesci vedono meglio di noi. E quindi rimandiamo il vetro, le lenti e la riflessione alla prossima puntata. Ovviamente, questo fenomeno nel suo complesso, ossia la deviazione del raggio luminoso quando passa da una sostanza a un’altra, prende il nome di rifrazione.

Prima di iniziare la cattura del pesce, il pescatore prende la canna da pesca e questa, senza volerlo, si immerge nel laghetto per metà. Il poveretto si accorge subito che essa sembra essersi piegata proprio in corrispondenza del punto C in cui tocca la superficie liquida. Accidenti con tutti i soldi che gli è costata è bastato immergerla nell’acqua perché si rompesse! Calma, calma. Non è successo niente di grave. E’ solo un’immagine virtuale, un’illusione visiva simile a un miraggio (parleremo anche di loro in seguito). E’ stata la rifrazione subita dalla luce che la canna immersa manda verso di lui a causare questa specie di miraggio.

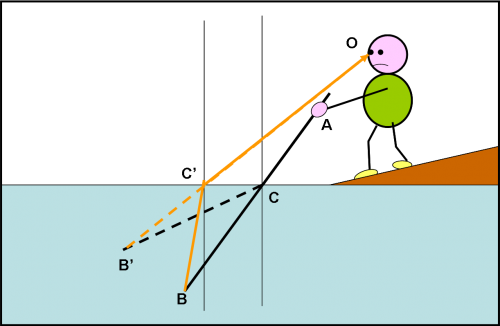
Lo vediamo bene nella Fig. 5. La canna AB è in realtà sempre dritta. Tuttavia il raggio di luce che parte dall’estremità B immersa nell’acqua viaggia verso l’esterno lungo il raggio BC’. Appena tocca la superficie in C’, esso è costretto, però, ad allontanarsi dalla perpendicolare z, a causa della rifrazione della luce, e quindi a seguire la linea C’O, fino a colpire l’occhio del pescatore. Egli, quindi, immagina di vedere la parte sommersa della canna nella direzione C’B’ e non in quella vera CB. In altre parole, il punto B viene spostato dalla rifrazione in B’. In conclusione la canna che appare all’occhio segue la linea spezzata ACB’. Finché è nell’aria appare normale (AC), poi si piega fino ad arrivare in B’. Almeno questo è quello che percepisce il suo occhio. Se il pescatore conoscesse un minimo di ottica non si sarebbe certo spaventato, ma a lui interessa solo pescare, usando magari le canne e le esche più sofisticate presenti in commercio, l’ottica non gli serve a niente.

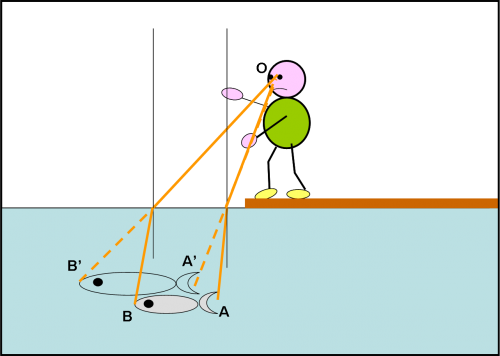
Il pescatore solleva la canna dall’acqua con grande rabbia, ma si accorge che è ancora perfettamente integra. Meno male: che spavento! Sicuramente è stato uno scherzo di un maledetto pesce! si riprende dallo shock e si rilassa. Comincia a guardare nel lago ed ecco comparire un pesce veramente eccezionale. Un vero mostro! Ma è proprio così grande? Consideriamo la Fig. 6. Il pesce “reale” è AB. Tracciamo i raggi luminosi che dalle due estremità del pesce vanno verso il pescatore. Sono quelli arancioni rappresentati dalle linee continue. Esse vengono rifratti con le modalità ormai ben conosciute e giungono all’occhio del pescatore lungo le direzioni B’O e A’O, Al pescatore il pesce AB apparirà nella posizione A’B’, un poco più in alto rispetto al fondo ma, soprattutto, molto più grande. Che preda! Anche se non riuscirà a catturarlo potrà dire ai suoi amici che era veramente una … balena!

Il pesce, comunque, non ha finito di prendersi gioco del pescatore. Quest’ultimo si accorge di essere troppo vicino al pesce e teme che lo possa vedere. Si allontana di qualche metro e allunga solo la canna. Povero illuso. Sembra proprio uguale ai bambini che giocano a nascondino e pensano di essere al sicuro da occhi indiscreti chiudendo gli occhi e voltandosi verso il muro.

L’ultimo capolavoro del pesce lo vediamo nella Fig. 7. Il pescatore è uscito addirittura dalla figura e si sente molto scaltro. Tuttavia cosa vede realmente il pesce? Ricordiamoci la Fig. 4 e il famoso angolo critico. Un raggio che arriva al pesce con un angolo di 49° deve aver viaggiato nell’aria proprio lungo la superficie. In altre parole il pesce vede entro 49° ciò che all’esterno è compreso in 90°, ossia dallo zenit al terreno. Se poi il pesce guarda dall’altra parte, a sinistra della perpendicolare alla superficie, riesce facilmente a vedere la stessa cosa ribaltata. Ne consegue che con due rapide occhiate il pesce riesce a vedere tutto ciò che succede intorno a lui anche a grande distanza: la sua vista copre un angolo di 180° nel piano della figura o, meglio, di 360° nella realtà tridimensionale. Il povero pescatore sarà perfettamente visibile e il pesce si guarderà bene dall’ingoiare qualcosa che proviene dalla sua direzione. Il campo di cista limite del pesce è segnato dai raggi rossi. Per raggi ancora più inclinati (linee nere) la luce torna indietro nell’acqua.

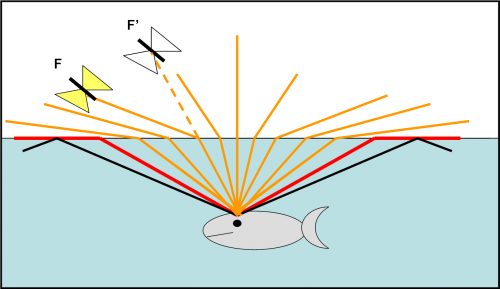
Qualcuno potrebbe dirmi: “Il merito non è del pesce, ma della rifrazione che gioca a suo favore. Ammettiamo pure che il pescatore sia molto ignorante in ottica e non capisca assolutamente quanto gli potrebbe essere utile durante il suo hobby. Tuttavia, non è più ignorante del pesce che sfrutta soltanto una serie di situazioni a lui favorevoli”. Ne siete proprio sicuri? Immaginiamo che ci sia una ghiotta farfallina sopra il laghetto. Il pesce la vede distintamente. Tuttavia, la vera posizione dell’insetto è in F, mentre l’immagine che appare al famelico predatore degli abissi è F’.

Il pescatore se ne accorge (anche se forse è pretendere troppo da un uomo normale…) e gioisce tra sé e sé: “Tu mi hai fregato, ma adesso sarai pagato con la stessa moneta.” Una piccola vendetta, tipica della miseria intellettuale di molti uomini odierni. Con grande meraviglia del pescatore, invece, il pesce salta con perfetto tempismo e inghiotte al volo la farfallina. Sembra quasi che durante la ricaduta in acqua strizzi l’occhio al pescatore che si crede tanto furbo con le sue attrezzature di ultima generazione, piene di sigle e di codici. Il pesce ha tenuto in conto la rifrazione anche se è solo un pesce… Un concetto insito in chi vive a continuo contatto con la Natura. L’uomo, invece, schiavo ormai della tecnologia a scatola chiusa, non c’è riuscito!

Fermiamoci qui. La prossima volta passeremo a vedere cosa succede al nostro raggio quando attraversa il vetro e capiremo l’importanza e la semplicità di un telescopio a lente.

//