Quante dimensioni ci sono nello spazio – tempo?

Alice e Bob sono colleghi in uno studio legale di New York. E sono anche amanti. Combinano un appuntamento segreto in un albergo poco conosciuto a Manhattan. “E’ all’angolo tra 58ma strada e 12ma Avenue,” sussurra Alice non appena si trovano entrambi davanti alla fotocopiatrice dell’ufficio. “Ci vediamo agli ascensori all’ottavo piano.” Bob sorride e annuisce.

Alice ha specificato la posizione del loro incontro assegnando tre numeri: 58, 12 e 8. In alternativa, (se magari i due amanti fossero stati professori di geografia) Alice avrebbe potuto usare latitudine, longitudine e altitudine. Il punto è che con tre numeri, possiamo risolvere in modo univoco un determinato punto dello spazio, e per questo motivo diciamo che lo spazio è tridimensionale.

Come Bob si volta, si rende conto c’è una cosa da risolvere. “A che ora, Alice?”

“Stasera, alle 19:00”,  risponde.

Con l’aggiunta di un quarto numero (7, o 19 per chi preferisce un orologio con 24 ore), il convegno di Bob e Alice è un evento pianificato nello spazio e nel tempo, che i fisici chiamano lo spazio-tempo.

I fisici dicono che lo spazio-tempo ha quattro dimensioni. Ma, come con molte cose in fisica, questo non è così semplice come sembra. La natura tridimensionale dello spazio è così ovvia ed intuitiva che la maggior parte delle persone – anche degli scienziati – non smettono mai di pensarci.

Ma nel 1921, un matematico tedesco di nome Theodor Kaluza ha proposto che il nostro intuito ci aveva ingannato: ha suggerito che lo spazio ha in realtà quattro dimensioni, e quindi lo spazio-tempo è a cinque dimensioni piuttosto che a quattro dimensioni. È arrivato a questa bizzarra conclusione, scoprendo un’incredibile fatto matematico mentre giocava con la parte più importante della fisica del periodo: la teoria della relatività generale di Albert Einstein.

Kaluza aveva preso le equazioni della teoria di Einstein, che sono state formulate per essere applicate alle familiari quattro dimensioni dello spazio-tempo, e le ha riscritte per essere applicate invece a cinque dimensioni. Perché? Beh, è ​​il tipo di cosa fanno i matematici. Ma il risultato è stato sorprendente. Visto dal punto di vista normale (a quattro dimensioni), le equazioni di Kaluza si riducono a quelle della teoria di Einstein, ma con un ulteriore set di termini (che descrive la dimensione extra).

Sorprendentemente, questi termini corrispondevano esattamente alla descrizione dell’elettromagnetismo che James Clerk Maxwell aveva pubblicato decenni prima. Con l’aggiunta di una dimensione extra di spazio, Kaluza aveva, a quanto pare, accidentalmente unificato la gravitazione e l’elettromagnetismo, due delle forze fondamentali della natura.

C’era solo un intoppo con questa teoria a cinque dimensioni: dove è la dimensione spazio extra? Noi non la vediamo. Come abbiamo potuto trascurare qualcosa di così fondamentale? Una risposta è arrivata qualche anno dopo da un fisico svedese, Oskar Klein. Forse, pensò Klein, non notiamo la quarta dimensione dello spazio, perché è arrotolata fino a una estensione molto piccola.

Per capire cosa significa ciò, immaginiamo di visualizzare di lato una cannuccia, da una certa distanza. Sembra una linea unidimensionale. Solo ad un esame più attento vediamo che la linea in realtà è un tubo. Qualsiasi dato punto sulla ‘linea’ è in realtà un piccolo cerchio che fa parte del tubo. Klein ha affermato che la dimensione extra di Kaluza è nascosta così – e cioè che ciò che normalmente consideriamo punti senza dimensione nello spazio sono in realtà piccoli cerchi, l’aggiunta di una quarta dimensione troppo piccola da vedere o anche da notare negli esperimenti.

La teoria Kaluza e di Klein è rimasta una curiosità matematica per qualche decennio, ma nel 1970 alcuni fisici hanno cominciato a chiedersi se la loro idea poteva essere estesa dalle sole gravità ed l’elettromagnetismo ad includere anche le due forze complementari della natura: la forza nucleare debole e La forza nucleare forte. Sicuramente è possibile, anche se per incorporare queste forze più complicate dobbiamo aggiungere non solo una, ma almeno sei dimensioni extra, portando a 10 le dimensioni spaziali – ed a 11 le dimensioni in totale, se si conta il tempo.

Esattamente come nella proposta originale di Klein, le dimensioni extra potrebbero essere arrotolate – “compattificate” è il termine tecnico – ad una estensione molto piccola, molto più piccola di un nucleo atomico. A differenza di una singola dimensione supplementare, che può essere compattificata solo in un cerchio, ora ci sono più possibilità: per esempio, due dimensioni possono essere compattificate sia in forma di una sfera che di un toro (a forma di ciambella). Per sei dimensioni, il numero di combinazioni schizza alle stelle. Il modo particolare in cui le dimensioni sono compattificate incide sulle proprietà delle varie forze.

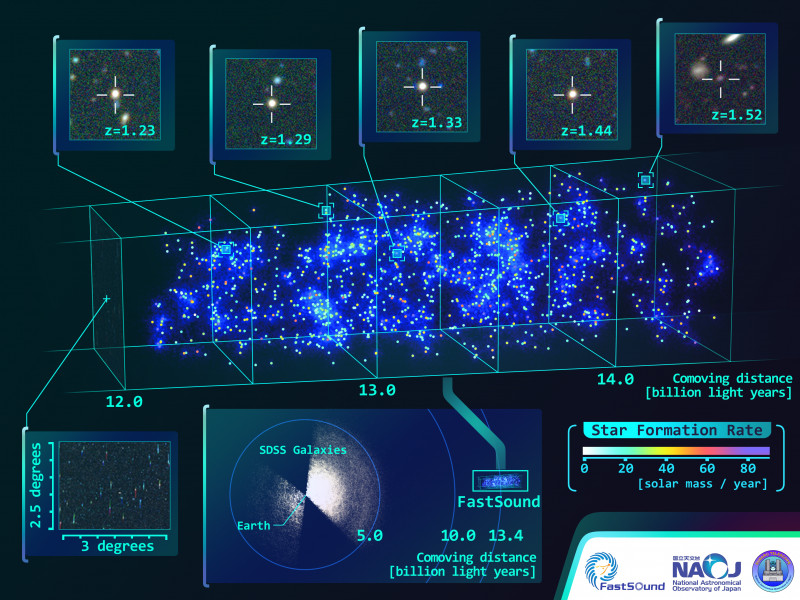
L’idea di base delle dimensioni extra invisibili ha trovato una accoglienza entusiasta tra i teorici delle stringhe. La teoria delle stringhe tenta di descrivere tutte le forze e le particelle della natura in termini di piccoli anelli di stringhe che guizzano in giro nello spazio-tempo a dimensioni superiori, con 11 dimensioni di spazio-tempo come ipotesi principale. La teoria delle stringhe è attualmente la favorita tra le teorie che mirano ad unificare la fisica fondamentale.

C’è voluto un bel po’ per far digerire l’idea che lo spazio-tempo ha più di quattro dimensioni, e per far sì che questa idea fosse accettata come un modello per lo spazio reale, ma oggi è considerata l’opzione di partenza. Se l’idea è giusta, allora la compattazione non è critica solo per la fisica, ma anche per gli amanti. La maggior parte di queste dimensioni sono arrotolate così strettamente che non ci si deve preoccupare di loro nella nostra vita quotidiana. Quindi dobbiamo solo ricordare quattro dimensioni, non 11 o più, per fissare un appuntamento!

Articolo originale di Paul Davies QUI.