Fin dagli albori della civiltà, l’uomo ha osservato il cielo. E fin dagli albori si è accorto che alcune stelle o pianeti erano più luminosi di altri. Iniziò quindi a classificarli in base alla loro brillantezza apparente. Il primo tentativo, puramente qualitativo, di misurare la luminosità stellare si deve a Ipparco di Nicea (II sec. a.C.). Purtroppo lui non aveva Celestia e il PC a disposizione.

Comunque, con l’aiuto soltanto della sua mente e dei suoi occhi, egli divise le stelle visibili a occhio nudo in sei grandezze. Le stelle più luminose erano dette di prima grandezza (m = + 1), quelle brillanti la metà di queste erano di seconda grandezza, e così via fino alla sesta grandezza (m = + 6), al limite della visione umana.
Il sistema prendeva in considerazione solo le stelle, e non considerava la Luna, il Sole o altri oggetti celesti non stellari. Tale sistema rimase valido fino al XIX secolo, quando con l’avanzare delle scienze astronomiche si richiedeva una maggiore precisione nella descrizione dei fenomeni, e quindi un metodo sicuro di misurazione della luminosità. Alla “grandezza” stellare venne sostituita la magnitudine.
Era ormai chiaro, però, che la magnitudine, ossia la grandezza di Ipparco, non rappresentava la vera luminosità stellare. Questo fatto è dovuto all’occhio umano che è sensibile alla luminosità in modo logaritmico. Ossia, percepisce le diversità di luminosità in modo molto meno appariscente di ciò che è in realtà. Pogson, nel 1856, decise di quantificare questa caratteristica stabilendo che: “Se una stella è 100 volte più luminosa di un’altra, questo fatto implica che tra le due vi siano esattamente 5 magnitudini di differenza”. In altre parole, l’occhio riceve un fattore 100 di incremento e lo recepisce solo come una differenza di 5 grandezze. Non è quindi difficile scrivere la formula ideata da Pogson, che mette in relazione le intensità luminose ricevute con le grandezze o magnitudini recepite dall’occhio umano:
m1 – m2 = – 2.5 log (I1/I2)
Infatti, se I1/I2 = 100 (I1 è 100 volte più luminosa di I2), si ha
m1 – m2 = – 2,5 log (100) = – 2,5 ∙ 2 = – 5
Il segno meno vuole solo significare che vengono considerate con magnitudine minore (una scelta storica e tuttora usata) le stelle più luminose. La magnitudine della stella 1 è più piccola di quella della stella 2. Nel caso precedente, la loro differenza è -5. D’altra parte tutti sanno che il Sole (l’oggetto più luminoso del Cielo) ha una magnitudine apparente di – 26.7, mentre la stella più debole visibile a occhio nudo (in condizioni perfette) è di magnitudine + 6.
Qual è il punto zero della scala delle magnitudini? Una volta si utilizzava la stella polare, assegnandole il valore di + 2, poi si è passati a considerare Vega come 0 della scala. Oggi si è scelta una media tra parecchie stelle. Tuttavia, l’importante non è tanto il punto zero, ma la differenza tra le magnitudini e quella non è cambiata. Teniamo anche presente che nei diversi colori cambiano le magnitudini e quindi il sistema di riferimento è molto più complicato di quanto non sembri. Esistono sistemi standard che legano tra loro le magnitudini alle varie lunghezze d’onda.
La formula precedente ci permette, in ogni modo, di ricavare la magnitudine di tutte le stelle, in base alla differenza di magnitudine rispetto a una stella che sia stata già correlata al punto 0 della scala.
La banalissima formula di Pogson ci permette anche (e soprattutto) di passare dalle magnitudini apparenti a quelle assolute, molto più importanti per l’astrofisica. Molto spesso, il metodo per ottenere la formula finale viene bellamente ignorato e si dà la formula finale di facilissima applicazione (come abbiamo visto nell’articolo su Celestia & Co.) Vediamo ora come si ottiene. Non è poi molto difficile e meriterebbe di essere descritta più spesso.
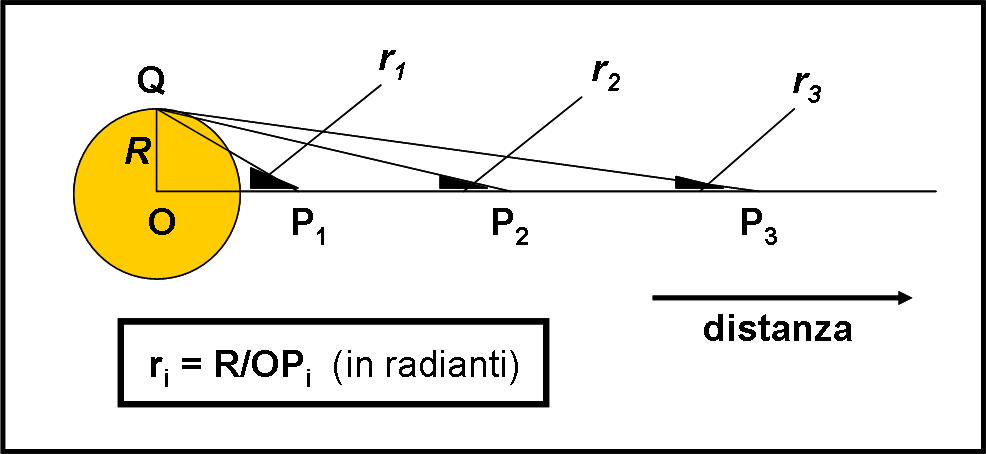
Torniamo alle luminosità vera delle stelle. La loro intensità I osservata da Terra è legata alla luminosità effettiva L attraverso una formuletta che tiene conto della distanza d percorsa dalla luce (ossia la distanza della stella). Più esattamente
I = L/ 4πd²
Andiamo a inserire questa relazione all’interno della formula di Pogson e otteniamo
m1 – m2 = – 2.5 log (I1/I2) = – 2.5 log (d22/ d12) = – 5 log (d2/d1)
Immaginiamo adesso che le due stelle siano, in realtà, lo stesso oggetto, però viste a due diverse distanze. Una è proprio quella rispetto alla Terra e l’altra è 10 parsec. Avremmo allora
m1 – m2 = – 5 (logd – log 10) = – 5 log d + 5
Ma m1 è la magnitudine apparente della stella vista dalla Terra (m), mentre m2 non è altro che la magnitudine che la stella avrebbe se fosse portata a 10 parsec, ossia la magnitudine assoluta M. Alla fine si ottiene quindi:
M – m = – 5 log d + 5
Che è la formula voluta e che, conoscendo la distanza d e la magnitudine apparente, ci permette di calcolare la magnitudine assoluta di una stella. Oppure, come nell’articolo su Celestia, il viceversa.
Elementare Watson!


Illuminante come al solito. Leggendo queste formule, che effettivamente sono semplicissime, mi rendo conto di come il mio cervello sia tragicamente abituato a elaborare le informazioni in modo figurativo "saltando" la rappresentazione geometrica e matematica dei concetti(che é alla base della loro "esistenza"). Urge trovare una soluzione! Grazie Enzo, continua a insistere, prima a poi la rotellina si sblocca
stampato ed aggiunto al precedente....
E' davvero curiosa questa cosa che l'occhio umano percepisce pari al logaritmo in base 10 del rapporto tra la luminosità effettiva delle due sorgenti moltiplicata per 2,5. Mi spiego come mai l'occhio segua proprio questa regola...
Viva l'occhio umano e la sua capacità di scegliere la via migliore e meno pericolosa....
Mi sei sempre più simpatico...
Ha sicuramente senso quello che hai detto ed è stupefacente vedere che qualità incredibili che abbiamo!
Però il mio dubbio si è risolto a metà, nel senso....perchè proprio il logaritmo? Sembra che la natura davvero parli in linguaggio matematico e non è solo un modo di dire...Quello che voglio dire, è che l'occhio non si limita ad attenuare la variabiltà della luminosità che riceve, ma lo fa proprio con una funzione logaritmica. Uno potrebbe dire: ovvio che ci deve essere un ordine nel funzionamento della retina e del cervello!
Però a me lascia comunque stupefatto tutto ciò...
Perchè il logaritmo? E se fosse che la funzione logaritmo (matematica) sia stata costruita e utilizzata proprio perchè creata dal corpo umano? Insomma, cambiamo l'ottica. Era così intelligente che la fisica si è adattata a inserirla tra le sue funzioni esplicative della realtà... Va beh... non facciamo i filosofi...
un abbraccio mattutino. tra poco lascio casa e mi faccio due ore di macchina per andare a comprare la migliore porchetta del Piemonte... Oggi grande festa eno-g-astronomia a casa mia!!!! Sarebbe bello ci fossi anche tu. Ti piace il vino???? Spero proprio di sì...
In realtà io tendo proprio a dormire poco e male per problemi di insonnia che mi porto dietro.
Beh di vini non sono certo un intenditore, ma se mi piacciono direi proprio di sì! Sicuramente il mio preferito è il rosso fermo e secco (soprattutto se di cantina
Allegato 609 Allegato 610
Come potete vedere, sono entrambi foto della nebulosa di Orione. Nella prima, i colori sono stati resi in modo lineare, nella seconda in modo logaritmico. E' evidente che nella seconda si colgono molti più dettagli che nella prima.
Il vantaggio evolutivo di una visone logaritmica dev'essere appunto questo.
Immaginate di dover evitare una minaccia nascosta: con la visione logaritmica avreste un miglior controllo delle differenze luminose, e potreste così cogliere meglio movimenti e evitare le minacce.....