Asteroidi: la magnitudine e la fase

Quando si osserva per diversi mesi un asteroide di fascia principale si nota chiaramente un incremento progressivo della sua magnitudine apparente, ovvero la magnitudine visuale dell’asteroide così come viene osservata dalla Terra. Occorre subito notare che la scala delle magnitudini è inversa e quindi un oggetto molto luminoso ha un valore della magnitudine inferiore rispetto ad uno meno luminoso. Ad esempio la luminosa stella Sirio ha una magnitudine di -1.5, Vega 0.0 e Castore 2.0.

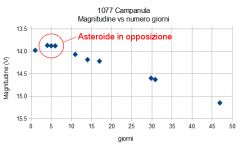
Adesso prendiamo ad esempio l’asteroide 1077 Campanula che ho osservato per più di un mese nel 2011. Il grafico di figura 1 mette in relazione la magnitudine apparente con il numero di giorni di osservazione trascorsi dalla prima sessione e ci mostra chiaramente un andamento prima crescente, fino al punto di opposizione (asteroide opposto al Sole), e poi decrescente man mano che l’asteroide si allontana dal punto di opposizione. I valori di magnitudine riportati nel grafico sono stati depurati dalle variazioni dovute all’andamento della curva di luce, causate dalla rotazione dell’asteroide intorno al proprio asse.

Facciamo un secondo passo, proviamo a mettere in relazione la magnitudine dell’asteroide con la sua distanza dalla Terra ed otteniamo il grafico di figura 2.

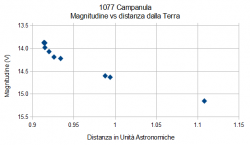
Per chi fosse interessato la posizione e la distanza degli asteroidi dalla Terra e dal Sole si può ricavare facilmente ed interattivamente, consultando la pagina web “NASA-JPL Small-Body Database Browser”->[Orbit Diagram] a questo indirizzo.

Notiamo che la magnitudine apparente dell’asteroide aumenta quasi linearmente con il crescere della distanza. Questo comportamento è piuttosto intuitivo e sperimentato anche nella nostra esperienza quotidiana, dal momento che a parità di luminosità, una fonte di luce più lontana ci appare anche meno luminosa.

Adesso ci è abbastanza chiaro che la magnitudine di un asteroide non è sempre la stessa ma varia in relazione a fattori esterni quali il tempo e la distanza. Per riuscire a comprendere meglio questi cambiamenti dobbiamo ricorrere ad una rappresentazione schematica (figura 3) dove si può vedere la configurazione geometrica del nostro asteroide 1077 Campanula al momento della prima ed ultima osservazione, rispettivamente del 17 settembre e del 2 novembre 2011.

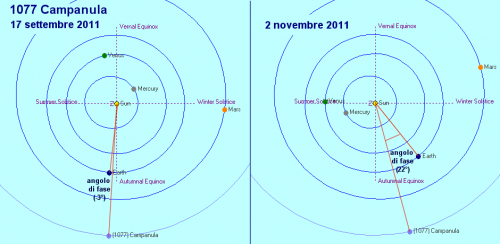
Ecco le considerazioni che possiamo fare guardando lo schema:

1. La distanza dell’asteroide varia rispetto alla Terra ed assume un valore minimo quando l’asteroide è in opposizione per poi crescere gradualmente al variare della configurazione geometrica asteroide-terra durante il percorso delle rispettive orbite.

2. L’angolo formato da sole-asteroide-terra (chiamato angolo di fase) è minimo durante l’opposizione e poi cresce progressivamente. Sostanzialmente l’asteroide ci mostra le fasi come succede con la Luna. C’è da dire quindi che quando l’asteroide è in opposizione (angolo di fase zero) il suo disco si presenta completamente illuminato in modo del tutto simile a quello che avviene con la Luna piena. Naturalmente il disco è così piccolo che non può essere risolto. Durante la fase piena “asteroide pieno” la superficie è completamente illuminata, le ombre sono assenti e la luce riflessa nella direzione della Terra è massima, in modo simile a quanto avviene con la luce riflessa da uno specchio. In queste condizioni la luminosità dell’asteroide è amplificata e questo effetto prende il nome di “effetto di opposizione” grazie al quale di solito è più facile scoprire gli asteroidi proprio quando sono in opposizione. Quando la geometria cambia e l’angolo di fase aumenta l’asteroide mostra verso la Terra solo una porzione del disco illuminato (come per le fasi lunari) riflettendo meno luce e mostrandosi così meno luminoso. Il valore massimo dell’angolo di fase per gli asteroidi di fascia principale, in relazione alle condizioni geometriche proprie dell’orbita della terra e dell’asteroide, non supera di solito i 20-30 gradi. Per una discussione più approfondita delle fasi e delle condizioni geometriche nelle quali si verificano si consiglia la lettura dell’articolo di Vincenzo Zappalà del 6 aprile 2013 “C’è chi riflette e c’è chi raccoglie: le fasi planetarie” a questo link.

Adesso che abbiamo individuato nella distanza uno dei fattori importanti che influisce sulla magnitudine apparente dell’asteroide possiamo provare a rimuoverne gli effetti, collocando l’asteroide convenzionalmente ad una distanza fissa di una unità astronomica dalla Terra ed una dal Sole.

Si tratta di una convenzione poiché questa configurazione geometrica non è rappresentativa della realtà. La magnitudine dell’asteroide, depurata dagli effetti della distanza, prende il nome di “Magnitudine Ridotta”.

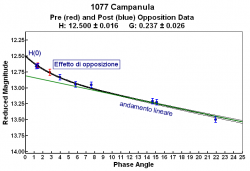
Applichiamo adesso il concetto di magnitudine ridotta al nostro asteroide (1077 Campanula) e vediamo cosa si ottiene. Il risultato è mostrato dal grafico di figura 4 dove troviamo la magnitudine ridotta messa in relazione con la fase.

Prendendo spunto dal grafico possiamo fissare alcuni concetti:

– Al crescere dell’angolo di fase, la magnitudine ridotta cresce e l’asteroide diventa sempre meno luminoso.

– La magnitudine ridotta nelle fasi inferiori a 7 gradi si impenna grazie al cosiddetto “effetto di opposizione”. La magnitudine ridotta tra 10 e 20 gradi ha invece un andamento lineare e la pendenza della retta di regressione prende il nome di “coefficiente di fase” ed è espresso in magnitudini per grado.

– La magnitudine ridotta alla fase zero prende il nome di magnitudine assoluta dell’asteroide H(0), da non confondersi con quella delle stelle. Questa è una grandezza molto importante che caratterizza la luminosità dell’asteroide e conseguentemente anche la sua dimensione, infatti un asteroide grande ha una magnitudine assoluta inferiore rispetto a quella di un asteroide piccolo. Ad esempio l’asteroide 4 Vesta ha una magnitudine assoluta H=3.2 ed un diametro di 520 km, mentre l’asteroide 1998 QE2, passato recentemente ad una distanza di circa 15 volte la distanza Terra-Luna, ha una magnitudine assoluta H=17.3 ed un diametro di 2.7 km (si è scoperto anche un satellite di 600 m).

– Nel 1985 l’ Unione Astronomica Internazionale adottò per gli asteroidi il sistema  denominato H-G allo scopo riuscire a predirne la magnitudine apparente ad ogni apparizione.

– Nel sistema H-G, H sta per magnitudine assoluta e G per “Slope Parameter”, un parametro che concorre a caratterizzare l’aspetto della curva di fase. Quest’ultimo varia anche sulla base della tipologia dell’asteroide. Ad esempio un valore basso di G (es: 0.09) è caratteristico degli asteroidi di tipo Carbonaceo, scuri e che riflettono poco la luce solare, mentre un valore alto di G (es: 0.4) è caratteristico degli asteroidi molto riflettenti, come ad esempio 4 Vesta. Nel nostro esempio l’asteroide 1077 Campanula, con un parametro G=0.24 si colloca nella tipologia degli asteroidi di media riflettività S o M, rispettivamente (Stony=rocciosi, M=metallici).

Dalla magnitudine assoluta possiamo ricavare il diametro dell’asteroide con la semplice relazione: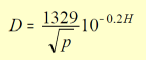  

Dove: H è la magnitudine assoluta (magnitudine ridotta a fase zero) e p è l’albedo geometrico dell’asteroide. Per albedo si intende il rapporto tra la luce incidente e la luce riflessa. Un corpo perfettamente assorbente ha albedo = 0 mentre un corpo perfettamente riflettente ha albedo = 1.

Gli asteroidi molto scuri di tipo carbonaceo hanno un albedo molto basso con un valore p=0.06 mentre asteroidi molto luminosi hanno un albedo alto con p=0.5. Per la tipologia S l’albedo medio è di 0.20, ne consegue che per l’asteroide 1077 Campanula possiamo stimare un diametro D = 9 km.

In conclusione, l’osservazione attenta e continua della luce di un asteroide ci può fornire un gran numero di informazioni. Possiamo determinare il suo periodo di rotazione attraverso la curva di luce e la sua magnitudine assoluta con la curva di fase, da cui poi si può ricavare la dimensione fisica. Infine il parametro G della curva di fase ci fornisce anche una indicazione approssimativa sulla sua classificazione tassonomica.

Spero quantomeno di aver stimolato l’interesse di qualcuno che abbia voglia di sperimentare questi concetti attraverso l’osservazione diretta degli asteroidi con la propria strumentazione. Serve solo un telescopio ed una camera CCD.