Giocando a nascondino: le occultazioni

In modo analogo a quanto fatto per la fase, cerchiamo di impostare la problematica in modo molto generale, ricavando poi le configurazioni più note come casi particolari. Definiamo occultazione il fenomeno in cui un corpo celeste si interpone fisicamente tra una sorgente di luce e un osservatore. Anche in questo caso i corpi in gioco sono essenzialmente tre: la sorgente di luce, il corpo che occulta e il corpo che viene occultato.

Se ci limitiamo agli oggetti del Sistema Solare, le situazioni che portano a una occultazione possono avvenire solo lungo la linea dei nodi o molto vicino ad essa. Ovviamente, qualsiasi retta va bene se le orbite sono complanari. Se invece estendiamo il discorso a tutto lo spazio, è meglio parlare più semplicemente di allineamento di corpi celesti. In ogni caso, però, lo schema che permette di determinare i parametri fondamentali per la risoluzione di tutti i casi è sempre la stessa ed è quella rappresentata in Fig. 1.

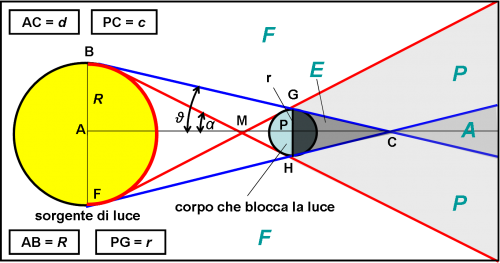
A sinistra vi è la sorgente di luce che può essere il Sole, ma anche un pianeta se consideriamo i suoi satelliti. Alla sua destra vi è il corpo occultante. Dalla sorgente di luce possono essere tracciate due coppie di rette. Quelle blu sono tangenti al corpo occultante (il cui diametro è considerato minore di quello della sorgente) e si incontrano nel punto C. La zona di spazio GHC (E) definisce il cono d’ombra del corpo occultante. Ogni osservatore contenuto all’interno di questo cono non è raggiunto dalla luce della sorgente. Il prolungamento delle rette blu delimita la zona A, in cui l’occultazione ha caratteristiche particolari, ma parte della luce raggiunge comunque l’osservatore. Per adesso limitiamoci alla parte geometrica. Le altre due rette sono quelle rosse che sono anch’esse tangenti al corpo occultante ma solo dopo essersi incrociate in M. Queste due linee determinano altre due zone di spazio: il cono P, che contiene al suo interno le due zone già trattate precedentemente e la regione di spazio F, esterna al cono P, luogo dei punti in cui l’osservatore non è influenzato dal corpo occultante, ossia riceve tutta la luce della sorgente.

Prima di descrivere cosa succede esattamente nei punti delle quattro zone, determiniamo geometricamente le grandezze che compaiono nella Fig. 1. Schematizziamola, allora, nella Fig. 2.

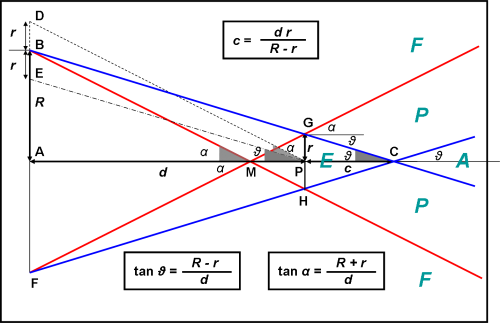
Vogliamo determinare l’ampiezza dei coni  E, A e P in funzione del raggio della sorgente R, del corpo occultante r e della distanza d tra di loro. Inoltre è interessante ricavare la lunghezza del cono d’ombra E, ossia c = PC.

L’ampiezza del cono d’ombra (linee blu) è dato dall’angolo ϑ. Un facile metodo per ottenere una soluzione immediata è quella di sottrarre al raggio R il raggio r, come indicato in figura. Il segmento AE è proprio R – r. Tracciamo la retta che unisce E con P. Dato che per costruzione il segmento DB è uguale a GP (raggio del corpo occultante), la retta EP è parallela a quella blu BG. Ne deriva che l’angolo EPA è uguale a ϑ. Dal triangolo EPA si ha subito:

tan(ϑ) = EA/AP = (R – r)/d

Ricaviamo adesso l’angolo α che caratterizza l’ampiezza del cono P. Questa volta, aggiungiamo r a R e otteniamo la retta DP che, per costruzione, è parallela a BM. L’angolo DPA è quindi uguale ad α. Dal triangolo DPA si ricava immediatamente:

tan(α) = DA/AP = (R + r)/d

Per i più “smaliziati”, queste due relazioni dicono che se d è molto più grande di R e r, gli angoli tendono a diventare zero e i raggi della sorgente di luce diventano paralleli: il cono d’ombra E diventa un cilindro e coincide praticamente con P. Ne parleremo ancora in seguito.

Non è difficile ricavare l’ultima grandezza che cercavamo: la lunghezza del cono d’ombra PC. Possiamo determinarla in vari modi. Ad esempio, considerando il triangolo GPC, si ha aubito:

c tan(ϑ) = r  e quindi:  c = r/tan(ϑ)

Oppure, dai triangoli simili AEP e PGC :

AE : PG = AP : PC,     ossia  (R – r) : r = d : c   e quindi:

c = d r/(R – r)

Ovviamente, le due relazioni sono analoghe e si ricavano una dall’altra ricordando le formule precedenti. In ogni modo, abbiamo risolto il problema e siamo in grado di applicare le formule a qualsiasi oggetto del sistema solare e non solo. Ricordiamo che potremmo benissimo sostituire alla sorgente luminosa un pianeta e al corpo occultante un suo satellite e poi spostare l’osservatore dove più ci piace. Le formule rimangono sempre le stesse.

A questo punto dobbiamo decidere dove porre l’osservatore. Solitamente lui è libero di muoversi nelle quattro zone definite precedentemente. Tuttavia, ha un certo interesse anche il caso in cui l’osservatore sia posto sul corpo occultante e guardi cosa succede a un corpo o a un punto che si muova nelle quattro zone. Questa situazione la vediamo nella Fig. 3 e ci permette di stabilire quanta luce della sorgente  raggiunge il punto “vagante” nello spazio. Sia O l’osservatore. Se il punto  si trova in E esso non riceve alcun raggio luminoso dalla sorgente. Per l’osservatore O è completamente scuro e teoricamente invisibile. Poniamo adesso il punto vagante in A. L’osservatore O lo vede, ma esso è illuminato solo da una parte della luce della sorgente luminosa, ossia quella che proviene dalle zone blu della sorgente, TV e UZ. Il resto della luce è bloccata dal corpo occultante. Ne deriva che il punto A è solo parzialmente illuminato e appare fioco. Analoga situazione capita quando il punto si trova in P. Esso viene illuminato solo dalla parte verde della sorgente luminosa, TY. Anche in questo caso l’osservatore O vede il punto P ma esso è parzialmente illuminato e quindi la luce riflessa è nuovamente fioca. Possiamo concludere che per un osservatore posto in O tutta la zona contenuta nel cono P (a parte quella contenuta anche in E) si trova in penombra. Se, infine, il punto vagante si porta in F , esso riceve tutta la luce della sorgente (TU) e la riflette completamente,  apparendo, quindi, più luminoso.

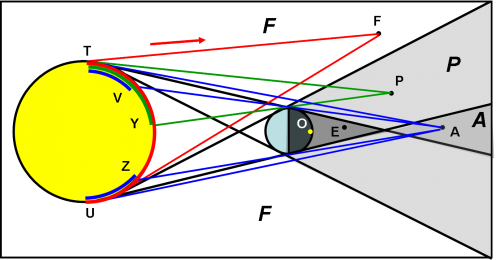
Finora abbiamo considerato un punto vagante. Ma al suo posto possiamo considerare un terzo corpo esteso. Non abbiamo certo bisogno di rifare la figura. Se il corpo esteso, ad esempio la Luna, si trova completamente all’interno del cono d’ombra E, essa non viene vista dall’osservatore O, posto sulla Terra, e si dice che la Luna è eclissata completamente dalla Terra. Se, invece, la Luna è immersa  nella zona P essa appare brillare di una luce più fioca e si dice che la Luna subisce un’eclisse di penombra. Teoricamente la stessa cosa succederebbe se la Luna riuscisse a spostarsi in A. L’osservatore O la vedrebbe brillare di una luce fioca.

Vi sono poi situazioni intermedie che dipendono dalle dimensioni e dalla posizione della Luna o, più in generale, del terzo corpo. Vi potete divertire a costruirvele da soli, ingrandendo o diminuendo le dimensioni della Luna e spostandola o avvicinandola alla Terra. In qualsiasi situazione sapreste esattamente descrivere le zone di ombra e di penombra che dipendono soltanto dalla sorgente luminosa (il Sole), dal corpo occultante (la Terra) e dalla loro distanza.

La realtà delle eclissi lunari la troverete come un caso particolare di una trattazione ben più generale e completa. Potrebbe sembrare che abbia voluto complicare le cose. Da un lato avreste ragione, ma lo scopo è quello di mettervi in condizioni di poter costruire tutte le possibili combinazioni che vogliate inventarvi.

Vediamo adesso la stessa configurazione da un altro punto di vista. L’osservatore è adesso il punto vagante nello spazio. Il corpo occultante può sempre essere qualsiasi, sia la Terra che la Luna o qualsiasi altro pianeta o satellite: basterebbe cambiare i raggi e la distanza tra sorgente e corpo occultante (e di conseguenza gli angoli dei due coni).

Diremo praticamente le stesse cose di prima, ma viste dall’altra parte, ossia da chi viene occultato e non da chi occulta. Cercate di capire bene questa differenza perché è estremamente importante anche se sembra trascurabile. Cosa vede il punto nella posizione E? Esso si trova all’interno del cono d’ombra e quindi non è raggiunto dalla luce della sorgente: vede, quindi, la parte in ombra del corpo occultante: si ha un’eclisse totale della sorgente di luce. Spostiamo, adesso, l’osservatore in A. Se per il corpo occultante quella era una posizione in cui il punto subiva solo un affievolimento di luminosità, per il punto vagante è invece una posizione molto particolare, in cui esso vede il disco del corpo occultante più piccolo del disco della sorgente di luce.

Infatti, guardando la Fig. 3, si nota che la luce che lo colpisce proviene da tutta la zona blu, che forma proprio un anello attorno al disco in ombra del corpo occultante. Un  disco nero, più o meno piccolo, all’interno del disco della sorgente luminosa. L’occultazione è solo parziale, ma dà luogo a un anello di luce, ossia a un’eclisse anulare della sorgente.

Se, invece, il punto si viene a trovare in P, esso vede solo una “fetta” della luce proveniente dalla zona verde della sorgente, come fosse in fase. Questa situazione, vista dal punto occultato, prende il nome di eclissi parziale. Infine, se il punto si trova in F, vede la sorgente completamente libera.

Se il punto vagante fosse sulla Luna, e il corpo occultante fosse la Terra, potremmo concludere che esso vedrebbe sicuramente eclissi totali di Sole causate dalla Terra. Ma vedrebbe anche eclissi anulari? E parziali? A voi la risposta… avete tutti i numeri e le formulette per rispondere.

E’ facile capire che se il corpo occultante fosse la Luna e il punto vagante si trovasse sulla Terra, i casi considerati precedentemente darebbero proprio luogo alle eclissi totali, anulari e parziali di Sole, dovute alla Luna. Il fatto che il disco oscuro della Terra  sia praticamente uguale a quello del Sole è un caso del tutto fortunato (basta calcolare la lunghezza del cono d’ombra lunare e confrontarlo con la distanza Terra-Luna e si scopre subito il perché). Divertitevi a far variare la distanza Terra-Luna mantenendo i raggi uguali: ne vedrete delle belle!

La situazione trattata finora coinvolge due corpi molto vicini e una sorgente di luce relativamente più distante. Una sua estrapolazione potrebbe essere applicata ai vari pianeti del Sistema Solare e ai loro satelliti. La figura non cambierebbe, ma, al variare delle distanze reciproche e dei raggi dei corpi, cambierebbero le condizioni di occultazione.

I pianeti interni, come Venere e Mercurio, possono benissimo prendere il posto del corpo occultante e il punto vagante può essere sulla Terra. Facendo i calcoli si vedrebbe che la Terra non potrebbe mai cadere all’interno dei loro coni d’ombra e quindi un osservatore su di essa vedrebbe solo eclissi anulari di  Sole dovuti ai dischi dei pianeti occultanti.  Queste occultazioni prendono solitamente il nome di transiti, dato che il disco planetario è estremamente più piccolo di quello del Sole. Un osservatore posto su Venere o su Mercurio vedrebbe, invece, delle eclissi di penombra della Terra.  Questo è un risultato a cui pochi pensano, ma è del tutto reale, anche se in pratica l’affievolimento luminoso è del tutto trascurabile. Potreste però calcolarlo facilmente..

Le cose cambiano ancora, ma solo apparentemente, se consideriamo come corpi occultanti i satelliti dei pianeti giganti. Che eclissi vedrebbero questi alieni o astronauti se fossero su Giove o su Saturno? Potete divertirvi quanto volete, dato che Giove e Saturno (ma anche Urano e Nettuno) hanno un mucchio di satelliti di varie dimensioni e distanze. Quanti causerebbero eclissi totali di Sole e quanti solo eclissi anulari? E nel caso di Plutone e Caronte?  E se il corpo occultante fosse il pianeta? Vedrebbero sparire i satelliti nella loro  ombra o ammirerebbero soltanto delle eclissi di penombra?

Potremmo anche osservare la situazione dall’esterno, ossia dalla Terra, ad esempio. Riusciremmo a vedere le eclissi di Sole dei satelliti su Giove o Saturno? Sicuramente sì, come da Giove o Saturno potremmo vedere le eclissi di Sole della Luna sulla Terra. Oppure vedere entrare i satelliti all’interno del cono d’ombra dei pianeti giganti o da loro vedere la Luna entrare in quello della Terra. O, ancora,considerare come sorgente di luce il pianeta e vedere i transiti dei suoi satelliti e viceversa. Tutti esempi che possono essere disegnati e risolti graficamente con le formule precedenti.

Il procedimento rimane analogo anche considerando due casi ben più generali in cui la sorgente  di luce è molto più lontana di quanto non sia il Sole o un pianeta. Di queste sorgenti ne abbiamo un numero incredibile a disposizione e sono le stelle del firmamento.

Il primo caso si ha quando  il corpo occultante è vicino all’osservatore; il secondo si ha quando il corpo occultante è vicino alla sorgente.

Vediamo insieme come varia la Fig. 1 nel primo caso. La stella è talmente lontana che i suoi raggi potrebbero benissimo essere considerati paralleli. Tuttavia, per mostrarvi che la Fig. 1 è sempre valida possiamo continuare a usarla, tenendo presente, però, che il cono d’ombra del corpo occultante ha una lunghezza tendente a infinito, ossia approssima un cilindro.

Consideriamo, allora, la Fig. 4. Non possono esistere zone di occultazioni anulari. Nemmeno di occultazioni parziali, dato che gli angoli ϑ e α tendono entrambi a zero. In altre parole, siamo limitati a considerare  solo la parte a sinistra dell’ipotetica linea verticale nera. In questa zona si verificano solo due casi: occultazione totale o nessuna occultazione. Le occultazioni totali sono notevoli, dato che la sorgente è puntiforme, mentre il corpo occultante ha dimensioni sicuramente superiori se visto da Terra, come rappresentato dal cono arancione. Il corpo occultante può essere la Luna, un pianeta, un suo satellite, un asteroide o quello che volete. Basta che abbia un diametro apparente visto da Terra più grande di un punto infinitesimo: molto facile.

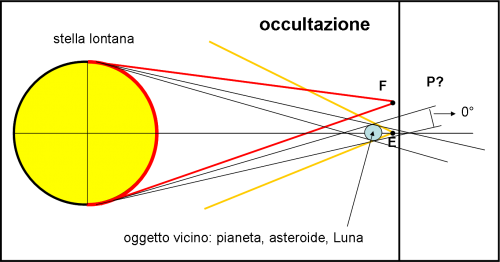
Ovviamente se l’osservatore si trovasse in F non vedrebbe nessuna occultazione. Queste configurazioni sono estremamente importanti e sono tuttora usate per vari motivi: determinare la forma di un asteroide, studiare l’atmosfera dei pianeti e dei loro satelliti, scoprire eventuali dischi di polvere, ecc. Oggi vi sono molte tecniche altrettanto o più accurate, ma fino a poco tempo fa le occultazioni stellari erano veramente fondamentali.

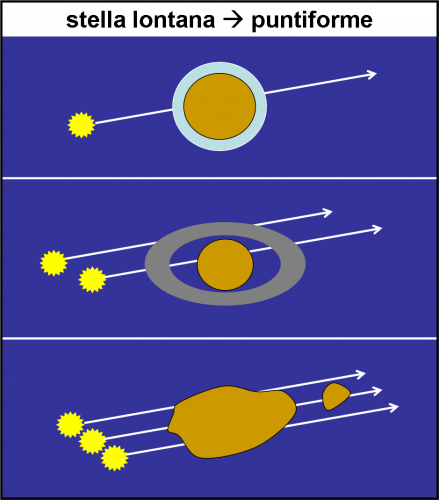
La Fig. 5 ne illustra tre casi esemplari. In alto l’occultazione di una stella da parte di un pianeta. La scomparsa più o meno improvvisa della stella dà informazioni importanti sull’eventuale atmosfera del pianeta. Nel mezzo, abbiamo l’occultazione di una stella da parte di un pianeta con un sistema di anelli. La scomparsa breve e temporanea della stella prima e dopo l’occultazione del pianeta permette di scoprire la presenza di anelli (e, in casi molto fortunati, di satelliti). Gli anelli di Urano e Nettuno sono stati scoperti in questo modo. In basso, abbiamo l’occultazione di una stella da parte di un asteroide di forma irregolare. Se gli osservatori sono tanti e ben distribuiti, ognuno assiste a una durata diversa dell’occultazione che permette di ricostruire la forma complessiva. Purtroppo, questi casi necessitano osservazioni distribuite su una zona piuttosto ristretta, con orologi perfettamente sincronizzati.  Gli unici in grado di compiere queste operazioni sono gli astrofili, ma i loro mezzi non sono mai stati veramente all’altezza dei requisiti necessari per ottenere un risultato sicuro e non controverso. Le occultazioni di questo tipo possono essere considerate a tutti gli effetti eclissi totali di una stella!

Ricordiamo anche che il corpo occultante potrebbe essere costruito “ad hoc” in modo da avere dimensioni apparenti simili a quelle della stella. In qualche modo stiamo parlando dei coronografi…

Consideriamo adesso il secondo caso, estremamente importante ancora oggi, anzi veramente fondamentale per la scoperta degli esopianeti.

La sorgente è sempre lontanissima (ossia è una stella), ma il corpo occultante è molto vicino a lei, ossia è un suo pianeta. La Fig. 3 resta identica, dato che le dimensioni della sorgente e del corpo occultante sono paragonabili alla loro distanza reciproca. Cambia invece la posizione dell’osservatore. Abbiamo, perciò, la Fig. 6. Essa è perfettamente identica alla Fig. 3, a parte il fatto che il punto vagante (l’osservatore) deve trovarsi abbondantemente a destra della linea verticale nera ipotetica. In altre parole, è abbondantemente al di fuori del cono di ombra del corpo occultante.

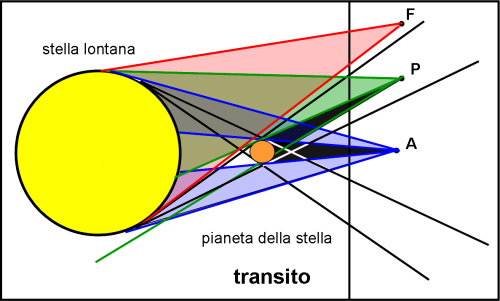
Se esso si trova in A vede un eclisse anulare, come rappresentato dal cono blu. Normalmente queste eclissi vengono chiamate transiti, dato che il corpo occultante è nettamente inferiore alla sorgente di luce. Tuttavia, il corpo occultante potrebbe essere una stella compagna della sorgente e allora si vedrebbero proprio delle eclissi mutue (binarie ad eclisse).  Un osservatore posto in P vedrebbe un’eclisse parziale (cono verde). Uno posto in F non si accorgerebbe di niente (cono rosso). In pratica, però, l’osservatore è talmente lontano che questi coni sono praticamente dei cilindri. Questo fatto implica che la perdita di luce dovuta alle eclissi è del tutto indipendente dalla distanza della stella. In altre parole, se si riesce a percepire la luce della sorgente, la perdita di luce è sempre la stessa frazione della luminosità totale. Questo è il sistema usato da Kepler, ovviamente.

Concludiamo con una considerazione puramente teorica, ma di un certo interesse. Se i coni dei vari colori tendono a essere dei cilindri a causa della grande distanza dell’osservatore, non lo sono di certo i coni relativi a sorgente e corpo occultante. In altre parole, gli angoli α e ϑ non tendono assolutamente a zero, dato che i raggi  possono essere comparabili e la distanza tra i due corpi relativamente piccola. Ne segue che un osservatore posto sul corpo occultante vedrebbe benissimo le quattro zone che avevamo definito nella Fig. 1. La Terra potrebbe, perciò, cadere tranquillamente in una di queste zone (esclusa ovviamente la zona E). In altre parole, la Terra subirebbe un’eclisse di penombra e apparirebbe meno luminosa se fosse in A e P rispetto a quanto succederebbe in F.

Ovviamente, questa è una considerazione del tutto teorica in quanto la luce di una stella lontana non riesce ad illuminare sufficientemente la Terra e della sua scomparsa nessuno si accorgerebbe se non stesse proprio guardandola… Solo per essere precisi…

Concludo qui e mi accorgo di avere probabilmente complicato dei concetti che sembravano ben più semplici. Tuttavia, lo scopo è un  altro. Chiunque sa come descrivere un’eclissi di Sole e di Luna o un transito di Venere e di Mercurio. Ci sono infiniti siti e libri che spiegano le configurazioni relative a questi fenomeni così eccitanti per l’astrofilo medio. Tuttavia, quanti sanno inserire tutte queste configurazioni in un contesto unico e generalizzato? Questo articolo vuole andare in questa direzione, ossia dare a chi vuole superare la semplice ammirazione di un dischetto nero che passa davanti al Sole o di una Luna appena più fioca del normale, la possibilità di ampliare i propri orizzonti e potersi calcolare da solo tutte le più strane configurazioni. Insomma, chi vuole pensare ha ora numerosissime occasioni per divertirsi con simulazioni strane e complicate.

Dopo aver letto questo articolo non ci sarebbe nemmeno bisogno di rispondere alle 7 domande 7. Tuttavia, è giusto che riporti le risposte, anche se molto sinteticamente.

Per gli interessati sono sempre a disposizione per spiegare meglio e ampliare quanto trattato.

1)      NO

2)      SI (solo anulare o parziale)

3)      Quando sono entrambe sulla linea dei nodi delle loro orbite

4)      SI (ma solo di penombra)

5)      SI (ma solo di penombra)

6)      La stessa configurazione di  (5) vista dalla Terra

7)      TUTTI quelli esterni e i loro satelliti

I pochi (come mai?) che hanno risposto sono andati piuttosto bene. Qualche problema solo sulla domanda (4)… vedremmo solo un’eclisse di penombra della Terra, ma sicuramente un’eclissi totale di Sole.